Intro

In this brief part of the waves series, we will be defining the concept of impedance of a string. Impedance is an important concept in many physical systems, as it will usually impact how much energy you are able to transmit across certain boundaries. Quite often in physics (and other fields), we're trying to solve problems where we need to do some sort of impedance matching. We will tackle this type of problem in a later post.

You may already be familiar with a type of impedance if you've studied electrical circuits. Indeed, you can find analogues (no pun intended) in electrical systems for most of the concepts involved here. We will also investigate this later, when we derive the wave equation for an electrical transmission line.

While I won't be continuing on from where we left off in Waves IV, I will assume that you know about everything we covered in the previous parts. You can find part 1 here.

Deriving impedance

Imagine again a stretched string along which a wave needs to be propagated. In order to create a sinusoidal waves of the form $y(x,t) = y(x\pm ct)$ (as investigated in part 2), we presumably had to apply some harmonic time-varying force, which we'll call $F_y$.

At any given moment in time, the applied force, $F_y$, must be whatever is required to balance the transverse component of the tension, $T$, on the string. This is shown here:

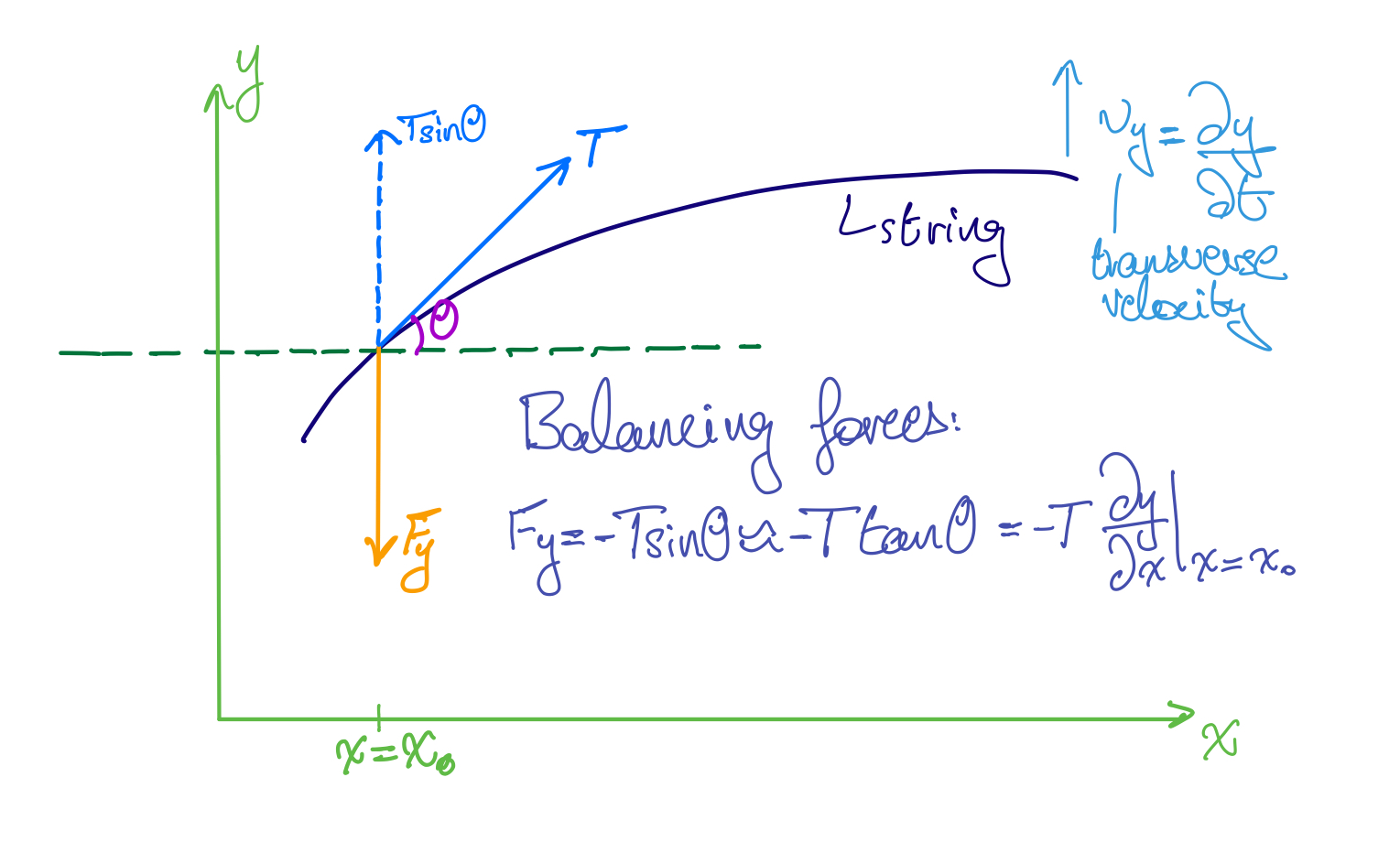
Forces at a point $x=x_0$ on a string.

We can balance the forces in this system at the point $x=x_0$ to get:

$$F_y = - T\sin \theta \approx - T\tan \theta = - T\frac{\partial y}{\partial x}|_{x=x_0}$$

Now, remember from Waves II, that for a constant-shape travelling wave moving in the positive x-direction with a solution of the form $y(x,t) = y(x - ct)$, we have the important relation:

$$\frac{\partial y}{\partial t} = - c\frac{\partial y}{\partial x}$$ $$\Rightarrow \frac{\partial y}{\partial x} = - \frac{1}{c} \frac{\partial y}{\partial t}$$

Substituting this into the expression for $F_y$:

$$F_y = \frac{T}{c} \frac{\partial y}{\partial t}|_{x=x_0}$$

Now, it's important to note that the expression $\frac{\partial y}{\partial t}|_{x=x_0}$ is exactly the transverse (vertical) velocity of the string at the point $x_0$, which we'll call $v_y$. So we can write:

$$\Rightarrow F_y = \frac{T}{c} v_y$$

Recall again that $c$, the speed of the waves on the string, is given by $c = \sqrt{\frac{T}{\rho}}$, so we can rewrite this as:

$$\Rightarrow F_y = \sqrt{T\rho} v_y$$

This quantity, $\sqrt{T\rho}$, is defined as the characteristic impedance of the string:

$$Z = \sqrt{T\rho}$$

This is because the definition of the mechanical impedance of a physical system is the ratio of the force applied at a point to the resulting velocity of that point. This is exactly our case. A force $F_y$ acts to balance the vertical component of tension on the string and results in a velocity $v_y$, such that:

$$\frac{F_y}{v_y} = \sqrt{T\rho} = Z$$

$$\Rightarrow F_y = Z v_y$$

In analogy to electrical circuits, this is the "Ohm's law" ($V = IR$) of the string on the wave! This is such that $F_y$ represents the voltage, $V$, $v_y$ represents the current in the circuit $I$, and Z, the impedance, naturally represents the resistance of a circuit element, $R$.

Relating to Power

Remember the final result from our consideration of power in Waves IV, which was:

$$P = \frac{1}{2} A^2\omega^2\sqrt{T\rho}$$

We can now rewrite this in terms of the impedance, $Z$:

$$P = \frac{1}{2} A^2\omega^2 Z$$

While we're here, and since we considered the transverse velocity of the string in this post, we can also consider a different definition of power to the one we took in Waves IV.

Consider the definition $P = Fv$ of power. In our case, $F$ is the transverse force acting on the string: $F = F_y$ and $v$, naturally, is the transverse velocity resulting from the force: $v = v_y$. From the equations derived above for $F_y$ and $v_y$:

$$F_y = - T\frac{\partial y}{\partial x}|_{x=x_0}, v_y = \frac{\partial y}{\partial t}|_{x=x_0},$$

we can write (omitting $x=x_0$):

$$P = - T\frac{\partial y}{\partial x}\frac{\partial y}{\partial t}$$

Applying again the relation $\frac{\partial y}{\partial x} = - \frac{1}{c} \frac{\partial y}{\partial t}$:

$$P = \frac{T}{c}(\frac{\partial y}{\partial t})^2 = Zv_y^2$$

This is again analogous to electrical circuits: $P = I^2R$!

Closing remarks

Thanks for reading! As always, I hope you found this post informative.

Feel free to message me with any questions you have about this topic either through the website or by leaving a comment below!

Happy Physics-ing!

Update (06/06/2018): Waves VI is now up, here.