Waves I: The Wave Equation for Waves on a String

Posted by Youssef Moawad on: 19/01/2018, in Physics

A new series!

Welcome to the first part of a new series about the physics of waves I'm starting. In my post about blog plans for 2018, I mentioned that I want to start writing about physics topics in a more mathematically rigorous manner. This is the start of this!

This series of posts will be largely inspired by topics I'm currently studying in my third year physics course at university and writing this will actually be a way of revision and of making sure I personally understand the concepts well. Hopefully, it will also be informative and enjoyable for the reader! Let's get started.

Waves on a String: Assumptions

For the purpose of deriving the wave equation for waves on a string, let's assume the following:

The string has a uniform linear density (length per unit mass in $m/kg$), $\rho$, throughout its length.
The string is held under a constant uniform tension, $T$.
The tension on the string is strong enough that the effect of gravity on the string is negligible.
The string can be thought of as a series of an infinite number of infinitesimally small coupled simple harmonic oscillators, which we'll call string elements, that vibrate up and down. As a result of the uniform tension on the string, each string element also experiences this force.
The tension acting on string elements does not change as they move transversely (up and down).

In order to write an equation that represents the wave motion on the string, we need to consider the forces acting on the string elements that make up the string and use Newton's second law to write the equation of motion for the string element.

Forces on a String Element

Consider the following string element of infinitesimal length, $\delta m$, and of mass $\delta m$:

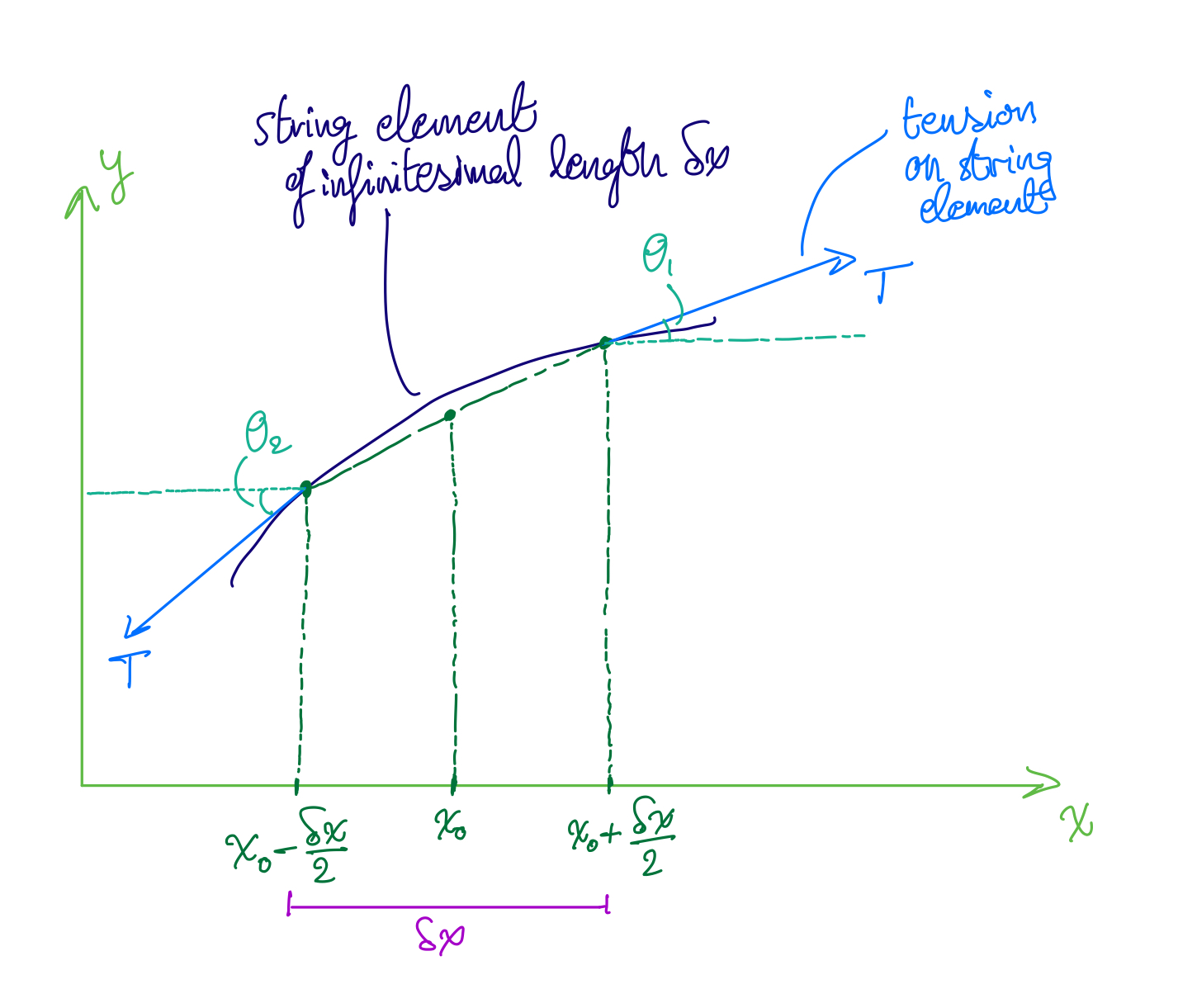
String element of length $\delta x$ and of mass $\delta m$.

Because the string has a linear density $\rho$, we can say that for the string element:

$$\rho=\frac{\delta m}{\delta x} \Rightarrow\delta m=\rho\delta x$$

We will need to use this substitution for $\delta m$ after applying Newton's second law.

Resolving forces horizontally

Resolving forces on the string element in the horizontal direction is indeed trivial as we are more interested in the transverse (vertical) movement of the string element, but it's included here for completeness. We indeed don't expect that the string elements themselves move horizontally because we model them as simple harmonic oscillators that vibrate only transversely.

Let the total horizontal force acting on the string element be $F_x$. Then we can see from the diagram above that there are two forces acting on the string in the horizontal direction: one in the positive direction equal to $T\cos(\theta_1)$, and one in the negative direction equal to $T\cos(\theta_2)$. Therefore, the total force acting on the string element in the horizontal direction is given by:

$$F_x=T\cos(\theta_1)-T\cos(\theta_2)$$

Now, if the displacement of the string is small enough, then both $\theta_1$ and $\theta_2$ will be small as well and we can apply a small angle approximation.

Side Note: Small Angle Approximations

Recall that in the limit that θ ≈ 0, we can say that:

$$\cos(\theta)\approx1$$ $$\sin(\theta)\approx\tan(\theta)\approx\theta$$

So using these results we can do the following approximations assuming both $\theta_1$ and $\theta_2$ are small:

$$\cos(\theta_1)\approx\cos(\theta_2)\approx1$$

And we can substitute these in the equation for $F_x$ to get:

$$F_x=T-T=0$$

As expected, the total horizontal force on the string element is zero and the string element does not move horizontally.

Resolving Forces Vertically

Side Note: Tangents at points on the string

Note that if we take the tangent to any point on the string where the angle between the tangent and the horizontal is θ, then we can say that:

$${\left.\frac{\displaystyle\partial y}{\displaystyle\partial x}\right|}_{x=x_0}=\tan\left(\theta\right)$$

To see this, consider the following diagram:

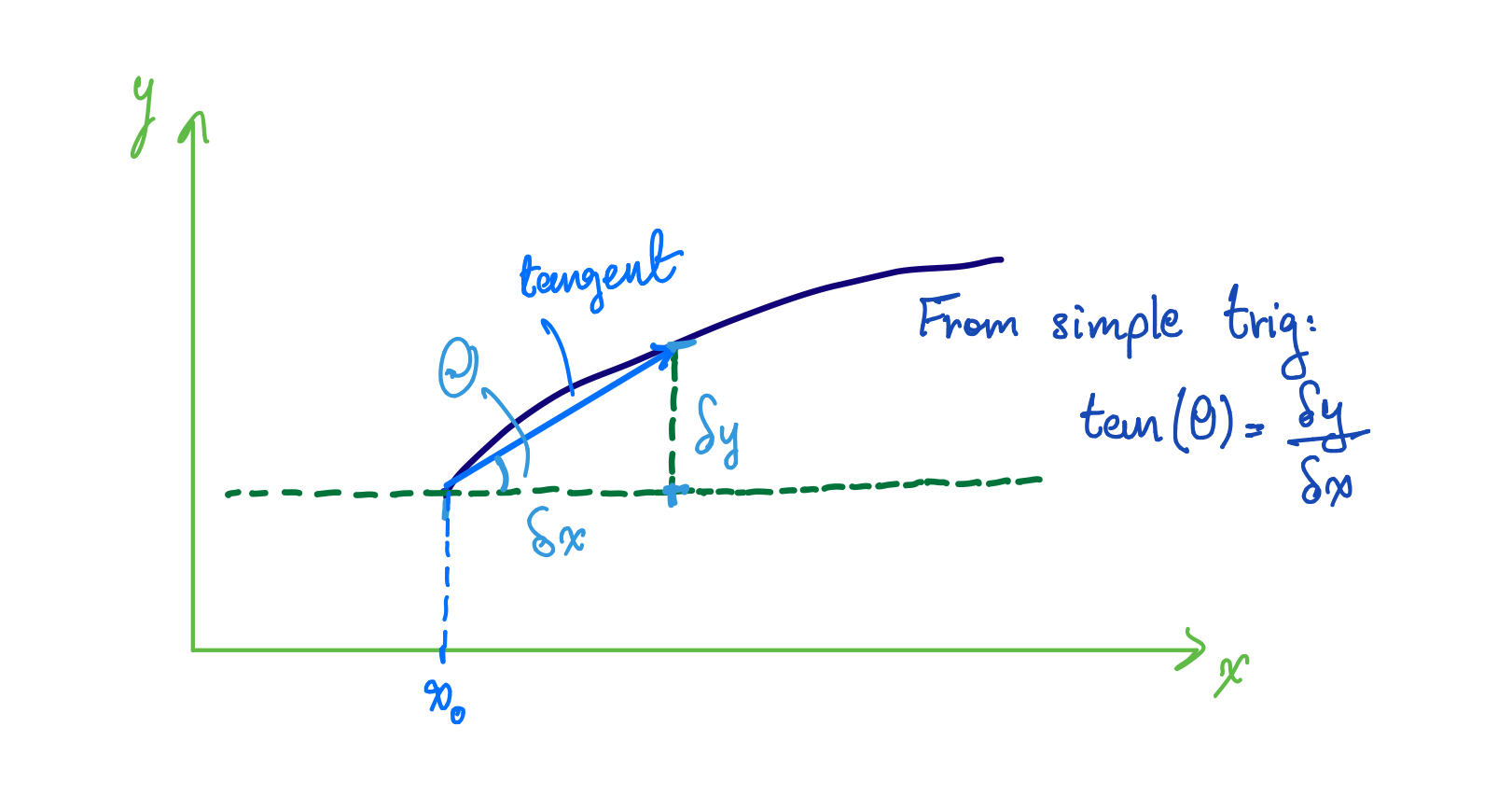
This arises from the trigonometry of taking the tangent at the point $x_0$.

From the diagram we can see that when the angle the tangent makes at the point $x_0$ is $\theta$, then through simple trigonometry, we can say:

$$\tan(\theta)=\frac{\delta y}{\delta x}$$

We can take the limit as $\delta x\rightarrow0$ and as $\delta y\rightarrow0$ and evaluate at the point $x = x_0$ to get the result above:

$${\left.\frac{\displaystyle\partial y}{\displaystyle\partial x}\right|}_{x=x_0}=\tan\left(\theta\right)$$

Let the total transverse force on the string element be $F_y$. We can now resolve the force in the vertical direction to get:

$$F_y=T\sin(\theta_1)-T\sin(\theta_2)$$

Now let's use the small angle approximation, $\sin(\theta)\approx\tan(\theta)$, to get:

$$F_y\approx T\tan(\theta_1)-T\tan(\theta_2)$$

From the result in the side note above, we can say that:

$${\left.\frac{\displaystyle\partial y}{\displaystyle\partial x}\right|}_{x=x_0+\frac{\delta x}2}=\tan\left(\theta_1\right),\;{\left.\frac{\displaystyle\partial y}{\displaystyle\partial x}\right|}_{x=x_0-\frac{\delta x}2}=\tan\left(\theta_2\right)$$

Plugging these into the expression for $F_y$:

$$F_y=T{\left.\frac{\displaystyle\partial y}{\displaystyle\partial x}\right|}_{x=x_0+\frac{\delta x}2}-T{\left.\frac{\displaystyle\partial y}{\displaystyle\partial x}\right|}_{x=x_0-\frac{\delta x}2}$$ $$=T({\left.\frac{\displaystyle\partial y}{\displaystyle\partial x}\right|}_{x=x_0+\frac{\delta x}2}-{\left.\frac{\displaystyle\partial y}{\displaystyle\partial x}\right|}_{x=x_0-\frac{\delta x}2})$$

Assuming the total transverse force on the string element is not zero, the string element will move with an acceleration $a$:

$$a=\frac{\partial^2y}{\partial t^2}$$

And we can now apply Newton's second law for the string element having mass $\delta m$:

$$F_y=\delta ma=\delta m\frac{\partial^2y}{\partial t^2}$$

But we know from the above that:

$$\delta m=\rho\delta x$$

So substituting for $\delta m$ and for $F_y$:

$$T({\left.\frac{\displaystyle\partial y}{\displaystyle\partial x}\right|}_{x=x_0+\frac{\delta x}2}-{\left.\frac{\displaystyle\partial y}{\displaystyle\partial x}\right|}_{x=x_0-\frac{\delta x}2})=\rho\delta x\frac{\partial^2y}{\partial t^2}$$ $$\Rightarrow\frac T\rho\frac1{\delta x}({\left.\frac{\displaystyle\partial y}{\displaystyle\partial x}\right|}_{x=x_0+\frac{\delta x}2}-{\left.\frac{\displaystyle\partial y}{\displaystyle\partial x}\right|}_{x=x_0-\frac{\delta x}2})=\frac{\partial^2y}{\partial t^2}$$

However, the expression $\frac{\displaystyle1}{\displaystyle\delta x}({\left.\frac{\displaystyle\partial y}{\displaystyle\partial x}\right|}_{x=x_0+\frac{\delta x}2}-{\left.\frac{\displaystyle\partial y}{\displaystyle\partial x}\right|}_{x=x_0-\frac{\delta x}2})$ is exactly the defining property for the second partial derivative of $y$ with respect to $x$: $\frac{\partial^2y}{\partial x^2}$. So we can write:

$$\frac{\partial^2y}{\partial x^2}\frac T\rho=\frac{\partial^2y}{\partial t^2}$$

And we finally arrive at the wave equation for a wave on a string!

Closing Remarks

The next step now is to determine the speed of the waves on the string, which we will find to be $c=\sqrt{\frac T\rho}$ in the next part of the series, which should be available here in the next few days (next week, most likely).

I hope you found this article informative and enjoyable! If there's anything you would like to discuss/ask for clarification about, feel free to leave a comment below or contact me through the website. I'm also open to suggestions and recommendations about the way I'm presenting the content and as a matter of fact, would appreciate any feedback. Thanks for reading!

Happy Physics-ing!

Update (25/01/2018): Waves II is now up, here.