Introduction

I have been an enthusiast of particle physics ever since my first encounter with the Standard Model of Particle Physics about 4 years ago. I was simply completely charmed by the way it explained the underlying reasons of common physical phenomena that I studied during my time in school. In this blog post, I am hoping to try to convey to you why I'm so fascinated by the Standard Model and the quantum theories that accompany it. I will attempt to explain everything assuming no prior particle physics knowledge on the reader's part.

As I was writing this article, I realised this is a very wide topic that should not be covered in a single blog article. So in this post, I'm going to mainly focus on the matter particles (the fermions) in the Standard Model after briefly considering fundamental forces and bosons and I will be writing more articles in the future exploring more topics.

I hope you enjoy this article!

Fair warning: I do not claim to be an expert on this topic. What I am discussing here is what I have come to understand regarding the Standard Model and particle physics through my own personal research into the topic and my studies at university.

Our universe and the forces that govern it

We start our journey by talking about the different ways by which matter interacts in our universe. Any kind of force that we experience in our daily lives can be categorised as one of four most fundamental forces. These four fundamental forces are:

• The Electromagnetic Force
• The Gravitational Force
• The Strong Nuclear Force
• The Weak Nuclear Force

The idea is, any sort of interaction that we experience in daily life is a form of one of these fundamental forces. For instance, when you push a box across the floor, there's three forces acting on it. There's the pushing force from your hands which is a manifestation of the electromagnetic force. There's the gravitational force exerted by the Earth on the box and finally there's the friction force which is another result of the fundamental electromagnetic force.

We usually do not see the results of the strong and weak nuclear forces in our daily lives because their very small ranges mean they can only come into effect on a subatomic scale. However, if you have studied radioactivity for example, you may know that Beta decay (where a neutron decays into a proton emitting an electron and a neutrino) happens through the weak force. We will have a look at these forces later.

Force mediators: The manifestations of the fundamental forces

In the Standard Model, each of the four fundamental forces has a hypothesised associated particle called the "force mediator" that goes along with it. Essentially these particles are what make the forces possible on a subatomic scale. The force mediators of each force are listed here:

• The Electromagnetic Force: mediated by the Photon
• The Gravitational Force: mediated by the Graviton (hypothesised)
• The Strong Nuclear Force: mediated by the Gluon
• The Weak Nuclear Force: mediated by the W and Z Bosons

With the exception of the graviton, all of the force mediators have been observed. The current issue with the graviton is that the force of gravity is very weak compared to the other forces. And so indeed the graviton is incredibly hard to detect, and to this day remains unconfirmed. But more on this later.

Matter

Now that we have briefly considered forces on a quantum scale, we can move on and have a look at matter. Most of us will know that, on a subatomic scale, matter is made up of protons, neutrons and electrons. Protons and neutrons are held together in the nucleus of an atom while electrons orbit the nucleus. But of what are these protons and neutrons made up, and, more importantly, why do they love sticking together in the nucleus, despite the protons having a positive electric charge? Surely the positive charge on the protons would mean they would tend to move away from each other. Thankfully, this is not the case! Later on, we will look at why protons do not cause nuclei to break up in this manner, but first, let's look at the main constituents of matter according to the Standard Model and we'll also look at the components of the proton and the neutron.

Quantum Numbers: A crash course

Before we delve into the world of quantum particles, let's very briefly discuss the properties that these particles can have.

Particles can have familiar properties such as mass, electric charge and intrinsic spin (the latter two of which are quantum numbers themselves). In addition to this, they can also have a bunch of other properties such as lepton quantum number and quark flavour number. For instance, an electron, which is the most common lepton, has an electron lepton number of +1. Similarly, an up quark has an upness flavour number of +1. A proton, which is a type of baryon, has a baryon number of +1.

These properties are known as quantum numbers, and they exist and are given to particles because (in most cases) they have to be conserved in particle interactions. An interaction here can be anything from a collision to a decay. The important thing here is that these quantum numbers are convserved, i.e. they have the same value across the system before and after the interaction. This happens for all the quantum numbers in all interactions, with the exception of the quark flavour numbers in a weak nuclear force interaction. The conservation law for the quark flavour numbers can be violated if and only if a weak interaction is taking place.

You will be able to appreciate the importance of quantum numbers further after we actually discuss the particles that can have these properties.

Antimatter

Very briefly, let's also introduce the idea of antimatter. For any particle, there exists an accompanying antiparticle. An electron has an antielectron (more commonly known as a positron); a proton has an antiproton; a hydrogen atom has an anti-hydrogen atom.

The idea is that these antiparticles have the same mass as their respective normal particles but have the opposite properties. For instance a positron (the electron's antiparticle) has a charge of +1 and an electron lepton number of -1. This makes sense because it is essentially the complete opposite of an electron. Similarly, an anti up quark has an upness of -1, and so on.

The Standard Model

Originally, I was going to have this section be a subsection of Matter. However, I thought this would be a little inappropriate because the Standard Model also explains the interactions between matter in terms of the force mediators discussed above.

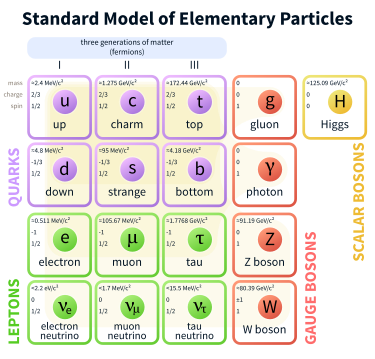
The Standard Model

Image from Wikipedia

The Standard Model predicts that everything in the universe is made up of two types of fundamental particles; fermions and bosons. The bosons in the Standard Model are the force mediators that we considered earlier, in addition to the, recently proven to exist, Higgs Boson (more on this later).

Fermions make up any matter that we can touch and are split into two types: quarks and leptons. Quarks mainly constitute the nucleons of atoms and have fractional electric charge (either 2/3 or -1/3, for matter quarks). Meanwhile, leptons have integer electric charge (either 0 or -1). Quarks and leptons come in three generations, also knows as families. You can see this in the above diagram of the Standard Model. The main difference between each generation is in mass. Each generation has a higher mass than the previous one; the third generation being the heaviest.

An imporant difference between fermions and bosons is that fermions have half-integer spin whereas bosons have integer spin. This means that particles that belong to the fermions can have spins of 1/2, 3/2, -1/2, -3/2...etc and particles belonging to the bosons can have spins of 0, 1, 2, -1...etc.

Quarks

There are six different types of quarks (in addition to their antiparticle counterparts). Each one has an associated quark flavour number which means that there are six different quark flavours. Every quark has a flavour number of +1 in its respective flavour, with the exception of the strange quark, which has a strangeness of -1. The quarks and their flavour numbers are outlined in this table (charge is also included as it will be discussed afterwards):

	Upness	Downness	Charm	Strangeness	Topness	Bottomness	Charge
Up Quark	1	0	0	0	0	0	2/3
Down Quark	0	1	0	0	0	0	-1/3
Charm Quark	0	0	1	0	0	0	2/3
Strange Quark	0	0	0	-1	0	0	-1/3
Top Quark	0	0	0	0	1	0	2/3
Bottom Quark	0	0	0	0	0	1	-1/3

As discussed in the section about antimatter, the antiparticles corresponding to these quarks will have the opposite quark flavour numbers.

Now, quarks are electrically charged particles. They are quite special however because they have electric charge of a multiple of 1/3. More specifically, up, charm and top quarks have a charge of 2/3 while down, strange and bottom quarks have a charge of -1/3. As you would expect, the antiquarks have charges of -2/3 and 1/3, respectively for each group.

The final quantum number we will consider is the baryon number. All quarks have a baryon number of 1/3 (with antiquarks having a baryon number of -1/3). The significance of this quantum number and this value will become apparent in the next section.

Protons and Neutrons

With an understanding of quarks under our belts, we can now have a look at how they combine to form baryons, specifically protons and neutrons. For now, we can simply define a baryon as a particle consisting of three quarks. Similarly, an antibaryon will consist of three antiquarks. Now the most common quarks are the ones in the first generation; the up and down quarks. This is because the heavier quarks in the second and third generations have a very short lifespan and often decay into quarks of the first generation.

Let's crack open a proton and look inside, shall we? Inside a proton, we find three individual particles; two up quarks and a down quark. Now, with the knowledge that a proton has a charge of +1 and is a baryon (i.e. consists of 3 quarks), we can arrive at this result. Start with 2 up quarks, now the charge is 4/3. This is too high and we definitely need another quark for this to be a baryon so try adding a down quark. Now the total charge is 4/3 - 1/3 = 1, which is exactly the electric charge of the proton.

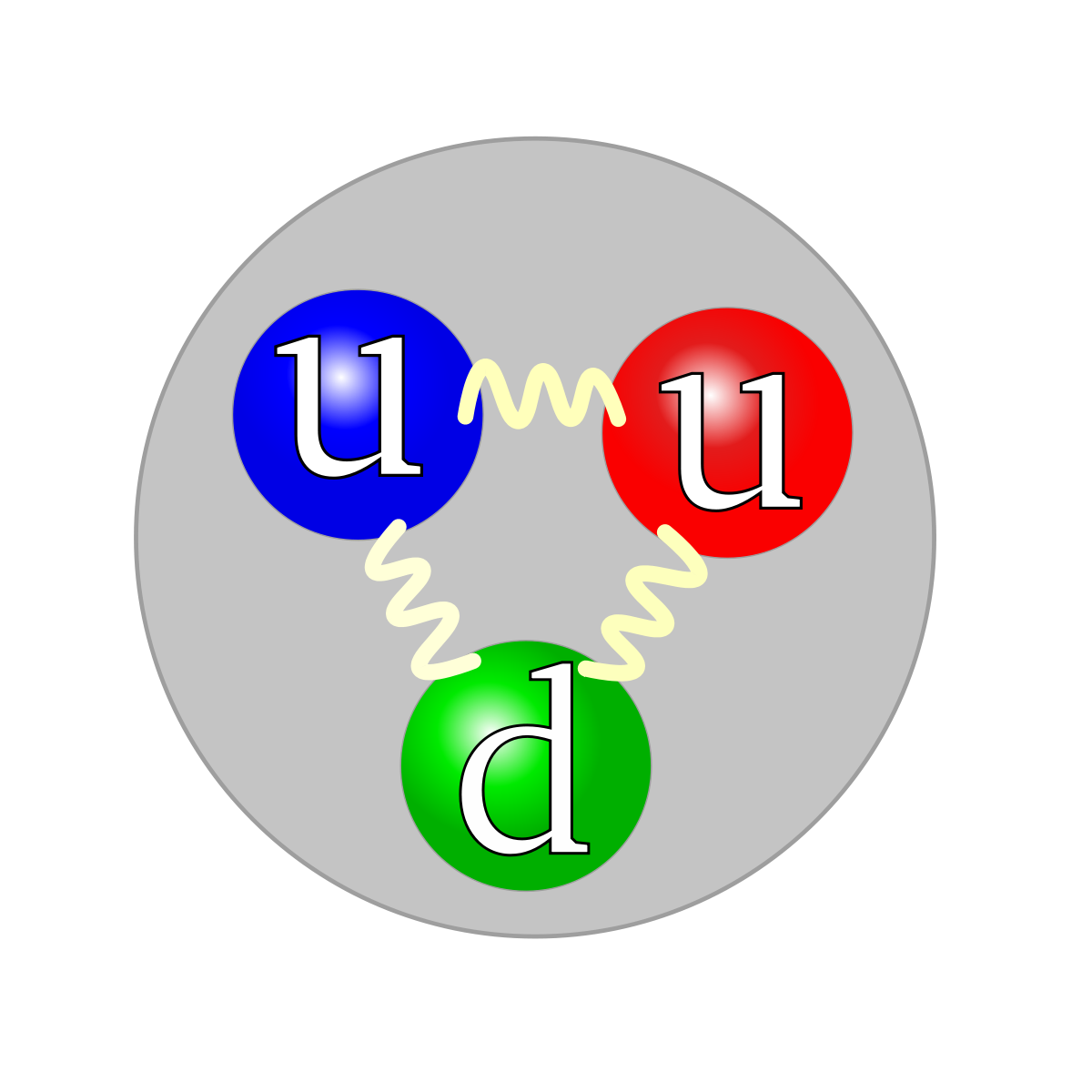
Quark composition of a proton

Image from Wikipedia

We can do the same for neutrons, which are also baryons. Now, neutrons are neutrally charged (i.e. have an electric charge of 0). So the total charge of the three quarks needs to cancel out. Start with an up quark, for a charge of 2/3. Now, can we add two more quarks to this such that the charges cancel? Indeed, adding 2 down quarks achieves just that. After adding 2 down quarks, the charge becomes 2/3 - 1/3 - 1/3 = 0 which is exactly the charge of a neutron. Therefore, we conclude that a neutron is composed of an up quark and two down quarks.

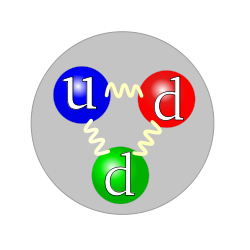
Quark composition of a neutron

Image from Wikipedia

A note on baryons and baryon numbers. Baryons, by definition, are composed of three quarks, each of which have a baryon number of +1/3. This makes sense because three of them come together to make something with a baryon number of +1, i.e. the baryon itself.

Personal note regarding electric charges

At the start of this article, I mentioned that I was charmed by the Standard Model around 4 years ago. Indeed, if I remember correctly, it was this charge analysis and composition of the proton and the neutron that initially brought my attention to the Standard Model. The fact that the Standard Model predicts the existence of the up and down quarks, each of which has just the right amount of charge to be able to combine with others to make particles that we knew so well (i.e the proton and the neutron) in such a perfect and coherent manner is what was mind-boggling to me at the start of this all. But I digress; let's get back to physics.

Leptons

There are three different types of leptons, each of which has a corresponding neutrino. The most familiar lepton is the electron, which most of us know to be usually found orbiting the nuclei of atoms. The other leptons are the muon and the tau. These are the heavier cousins of the electron and belong to the second and third generations of the fermions, respectively. Electrons, muons and taus all have a charge of -1 but they have different lepton quantum numbers. To each of these particles corresponds a neutrino which has the same lepton number number as the lepton to which it corresponds but has an electric charge of 0. These properties are demonstrated in this table:

	Electron Lepton Number	Muon Lepton Number	Tau Lepton Number	Charge
Electron	1	0	0	-1
Electron Neutrino	1	0	0	0
Muon	0	1	0	-1
Muon Neutrino	0	1	0	0
Tau	0	0	1	-1
Tau Neutrino	0	0	1	0

Neutrinos mainly come into interactions when it is needed to balance a lepton number with charge already being balanced. For instance, in Beta decay mentioned above, where a neutron decays into a proton, an electron and an antielectron neutrino are emitted. The electron is there to balance the positive charge on the proton but then it is also needed to balance the electron lepton number. So the antielectron neutrino is emitted as it has an electron lepton number of -1, thus neutralising the effect of the electron's +1 lepton number.

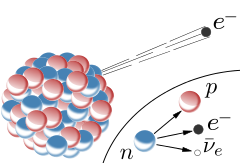
Beta decay. A neutron decays into a proton emitting an electron and an electron neutrino in the process.

Image from Wikipedia

Bosons

I will not be describing bosons in detail in this blog post but rather I will be writing seperate articles about each fundamental force (each of which has an associated boson(s)) and the quantum theory that describes it in the future.

The bosons in the Standard Model represent the force mediator particles of three of the four fundamental forces, in addition to the Higgs Boson. The electromagnetic force is mediated by the photon. The strong force is mediated by the gluon and finally, the weak force is mediated by the W and Z bosons. Now, we will very briefly consider the strong nuclear force.

The Strong Nuclear Force

The strong nuclear force is the one responsible for the nuclei of atoms not decomposing because of the repulsive forces between the protons. It binds nucleons together through pion exchange, where nucleons exchange particles called pions (which are made up of a quark and an antiquark) between them. Colour here refers to a different kind of charge that some particles, mainly quarks, can have.

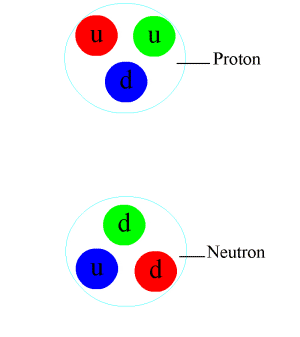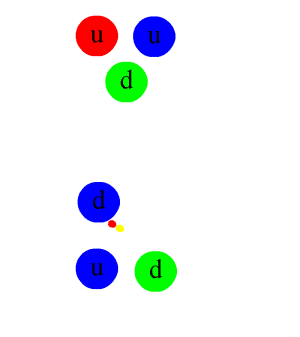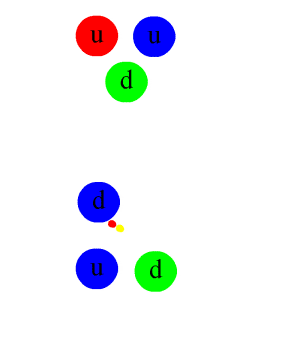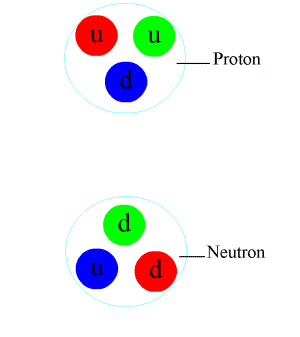
Pions being exchanged between a neutron and a proton

Image from Wikipedia

This will all be explained further in the next Particle Physics article, where we will consider the theory of Quantum Chromodynamics which is the theory that explains the strong nuclear force, colour charge and gluons.

Conclusions

I hope I have demonstrated some of the properties of the Standard Model that I personally find quite cool. At the start of this, I had intended to put everything I had to say into a single article. However, obviously this is such a massive topic, I realise it will require several articles to convey everything I want to.

We conclude this article with a recap. There are four fundamental forces of nature, each of which can be explained by the associated boson(s) on a quantum level. The matter that we see everyday is made up of fermions, mainly up and down quarks and electrons. Two up quarks combine with a down quark to make up a proton. An up quark and two down quarks make up a neutron. Heavier versions of all these fundamental particles exist, however they do not stick around for very long as they usually decay into the lighter particles.

I'm hoping to have the next article of this new series written and published here by next week when I hope you will be back to read it. Thank you for reading!

P.S.: As this is the first article of this kind of thing, please provide any feedback you can about what you enjoyed and what you did not enjoy and would like done better next time. Feel free to contact me about this or you can leave a comment here through the integrated Facebook comments. Your feedback is highly appreciated and will help to improve this blog!

UPDATE (23/04/2017): Part 2 of this series, titled Colourful Quantum Chromodynamics, is now live here.