Welcome back

This will be a very brief post, continiuing directly from the previous one, where I will be showing that the speed of waves propagating on a string is given by the relation:

$$c=\sqrt{\frac{T}\rho}$$

In the the last post, we showed that the wave equation is given by:

$$\frac{\partial^2y}{\partial x^2}\frac T\rho=\frac{\partial^2y}{\partial t^2}$$

In this post, we're going to consider a solution to this equation that represents a wave on the string that has a constant shape with time.

Second coordinate frame

Consider a string with a wave pulse propagating through it. Now let's imagine we define a second coordinate frame inside the main x-y frame, that moves with the pulse with the same speed. Call this the $x'$-frame. Assume the pulse moves with speed $c$, such that the $x'$-frame also moves with speed $c$.

Since this second frame is moving a constant speed, we can say that at any point the position of the origin of the $x'$-frame in the original frame is given by $x_f = ct$.

Let's visualise this:

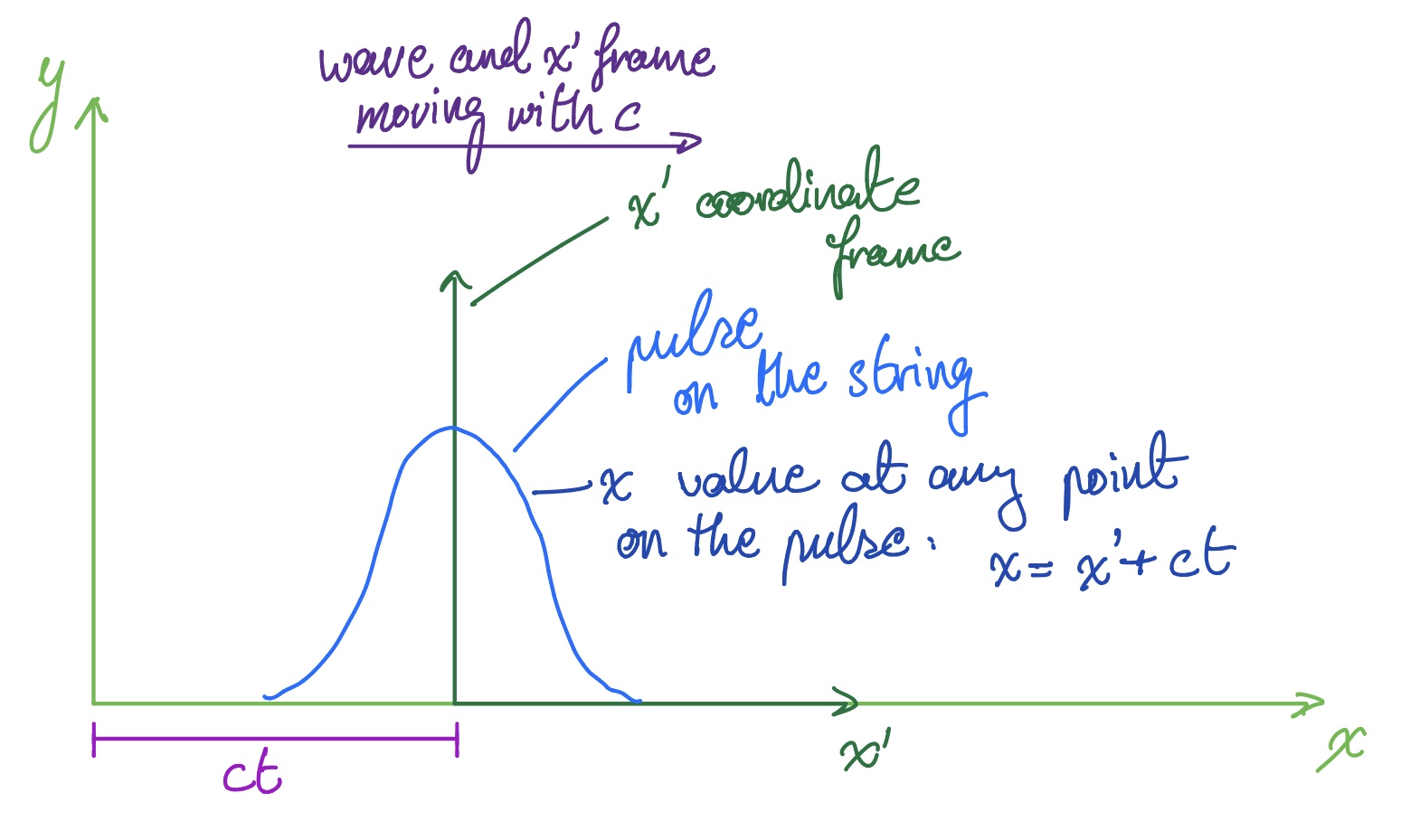
The $x'$-frame moves with a constant speed, $c$, same as the pulse. As such, any point $x$ on the pulse can be given by $x = x' + ct$.

Since at any point $t$ in time, the second frame has moved a distance $ct$ from the origin of the original frame, we can say that any point $x$ on the pulse is given by:

$$x = x' + ct$$ $$\Rightarrow x' = x - ct$$

Note that, if the wave is moving in the negative x-direction, then the frame will move with the opposite velocity, $-c$. For this case, we can say that $x = x' - ct \Rightarrow x' = x + ct$. It's just a sign reversal!

Now consider the $y$ position at any point on the wave pulse in the second frame. Since the the second frame is moving with the wave and the pulse is of a constant shape, then each $x'$ value on the pulse maps to a $y$ value; that is to say, $y$ depends only on $x'$.

From this, we can say that a solution to the wave equation, for this pulse moving in the positive x-direction, can be given by:

$$y(x,t) = y(x') = y(x-ct)$$

Similarly, for a pulse moving in the negative x-direction, we can say $y(x,t) = y(x+ct)$.

Beware: do not get confused! This is not saying that $y = x - ct$ is a solution to the wave equation but rather that there exists some function $y(x')$, where $x'=x-ct$, such that $y(x')=y(x-ct)$ is a solution to the wave equation.

Plugging our solution into the wave equation

We now have a solution to our pulse in the form of $y(x-ct)$. Let's plug this into the wave equation derived before for a string with linear density, $\rho$, and tension, $T$. To do this, we need to compute the second partial derivatives of $y$ with respect to $x$ and $t$. Define $u = x-ct$, such that:

$$u = x - ct$$ $$\Rightarrow y = y(u)$$

We can use the chain rule to define:

$$\frac{\partial y}{\partial t} = \frac{\partial y}{\partial u} \frac{\partial u}{\partial t},$$ $$\frac{\partial y}{\partial x} = \frac{\partial y}{\partial u} \frac{\partial u}{\partial x}$$

From $u = x-ct$, we find that:

$$\frac{\partial u}{\partial t} = -c, \frac{\partial u}{\partial x} = 1$$

Plugging this into the above:

$$\frac{\partial y}{\partial t} = -c\frac{\partial y}{\partial u},$$ $$\frac{\partial y}{\partial x} = \frac{\partial y}{\partial u}$$

Combining these, we get:

$$\frac{\partial y}{\partial t} = -c\frac{\partial y}{\partial x}$$

This is an important relation for a constant shape travelling wave, which we will likely use in later articles.

We can use the chain rule one more time on the expressions derived for $\frac{\partial y}{\partial t}$ and $\frac{\partial y}{\partial x}$:

$$\frac{\partial}{\partial t}(\frac{\partial y}{\partial t}) = \frac{\partial}{\partial u}(-c\frac{\partial y}{\partial u})\frac{\partial u}{\partial t}$$

We know that $\frac{\partial u}{\partial t} = -c$, so:

$$\Rightarrow \frac{\partial^2y}{\partial t^2} = c^2 \frac{\partial^2y}{\partial u^2} $$

Doing the same for $\frac{\partial y}{\partial x}$:

$$\frac{\partial}{\partial x}(\frac{\partial y}{\partial x}) = \frac{\partial}{\partial u}(\frac{\partial y}{\partial u})\frac{\partial u}{\partial x}$$

Again, we know that $\frac{\partial u}{\partial x} = 1$:

$$\Rightarrow \frac{\partial^2y}{\partial x^2} = \frac{\partial^2y}{\partial u^2} $$

We can combine this expression with the one for $\frac{\partial^2y}{\partial t^2}$, to get:

$$\frac{\partial^2y}{\partial t^2} = c^2\frac{\partial^2y}{\partial x^2}$$

Now, compare this with the wave equation we derived before:

$$\frac{\partial^2y}{\partial x^2}\frac T\rho=\frac{\partial^2y}{\partial t^2}$$

From simple inspection, we can see that $c^2=\frac{T}{\rho}$, which gives us:

$$c^2 = \frac{T}{\rho} \Rightarrow c=\sqrt{\frac{T}{\rho}}$$

This is the result we expect.

Closing Remarks

Thanks for reading! I hope you found this post informative.

I'm trying to get into the habit now of writing these shorter, much more focused articles. This post in particular is mostly about the maths, which is simple enough, but it requires close attention to be understood well.

Because this is a very fresh format for this blog, I'd very much appreciate your feedback and any suggestions for improvement. In particular, do you think I should include more/less detail and comment about the mathematics? Please do let me know. There's the comments section below and you can always message me through the site.

Also, please don't hesitate to get in touch with me with any questions.

Happy Physics-ing!

Update (05/02/2018): Waves III is now up, here.