Wave Energy
This post carries on from the discussion in the previous two: Waves I and Waves II. It's recommended to have a look at those if you haven't already.
Any wave on a string (and any in general) will transport energy. As in all physical situations, we can consider the two different forms of energy carried by the wave: kinetic and potential energy. The sum of these two parts gives the total energy transported by the wave.
To do this, we will again consider the string to be formed of an infinite number of simple harmonic oscillators represented by string elements of infinitesimal length, $\delta x$, and infinitesimal mass, $\delta m$, as described in Waves I.
The kinetic energy of the string element arises from the fact that the string element moves transversely, or up and down, with a velocity $v_y$ (but not horizontally; remember that the string elements themselves do not move through the string). The potential energy results because the string element is stretched from its natural length by the wave. This is elastic potential energy.
Side note: Kinetic and Elastic Potential Energy
Remember that the kinetic energy of an object with mass $m$ and moving with velocity $v$ is given by:
$$K = \frac{1}{2}mv^2$$
The elastic energy stored in a string element is a result of the work done by the tension on the string element. For a string element of infinitesimal length, under tension $T$ that is stretched by $\Delta x$, this is given by:
$$V = T\Delta x$$
Side note: Energy density
It is helpful to be familiar with the concept of energy density. An energy density represents how the energy is distributed across some medium. In our case, the medium is a string and we will be interested in how the energy is distributed across its length. This would be the energy per unit length of the string. For instance, the kinetic energy density of the string is $\frac{dK}{dx}$. If we have an expression for this, we can integrate with respect to $x$ and obtain an expression for the total kinetic energy of the string. We can also do a similar treatment to potential energy density, $\frac{dV}{dx}$, and we can indeed add the energy densities up to obtain the total energy density of the string, $\frac{dE}{dx}$.
Kinetic energy of a wave on a string
Let's start my considering the kinetic energy of a string element. As mentioned above, the string element is under a tension, $T$, and has an infinitesimal length of $\delta x$ and mass $\delta m$. The entire string has a linear density of $\rho$ so we can say that:
$$\rho = \frac{\delta m}{\delta x} \Rightarrow \delta m = \rho \delta x$$
The string element is moving transversely with velocity $v_y = \frac{\partial y}{\partial t}$ and does not move horizontally, so the kinetic energy of the string element, $\delta K$ is given by:
$$\delta K = \frac{1}{2}\delta m v_y^2 = \frac{1}{2}\rho\delta x (\frac{\partial y}{\partial t})^2$$
Now let's divide by $\delta x$ and take the limit as $\delta x \rightarrow 0$ to get $\frac{dK}{dx}$.
$$\Rightarrow \frac{\delta K}{\delta x} = \frac{1}{2}\rho (\frac{\partial y}{\partial t})^2$$ $$\Rightarrow \frac{dK}{dx} = \frac{1}{2}\rho (\frac{\partial y}{\partial t})^2$$
This is the kinetic energy density of the string. We can integrate this to find the total kinetic energy on the string:
$$K = \int \frac{1}{2}\rho (\frac{\partial y}{\partial t})^2 dx = \frac{1}{2}\rho \int (\frac{\partial y}{\partial t})^2 dx$$
This expression gives the total kinetic energy of the waves propagating on the string. We will now consider the potential energy, which we will be able to add to the kinetic energy to get the total energy of the string.
Potential energy of a wave on a string
As mentioned above, the potential energy arises because the string element is stretched from its natural length by the wave.
To apply the formula mentioned above, we need to determine the extension of the string element. This will be the difference between its stretched length (call this $(\delta x)'$) and its natural length, $\delta x$. Let's visualise the stretched string element to understand this more clearly:
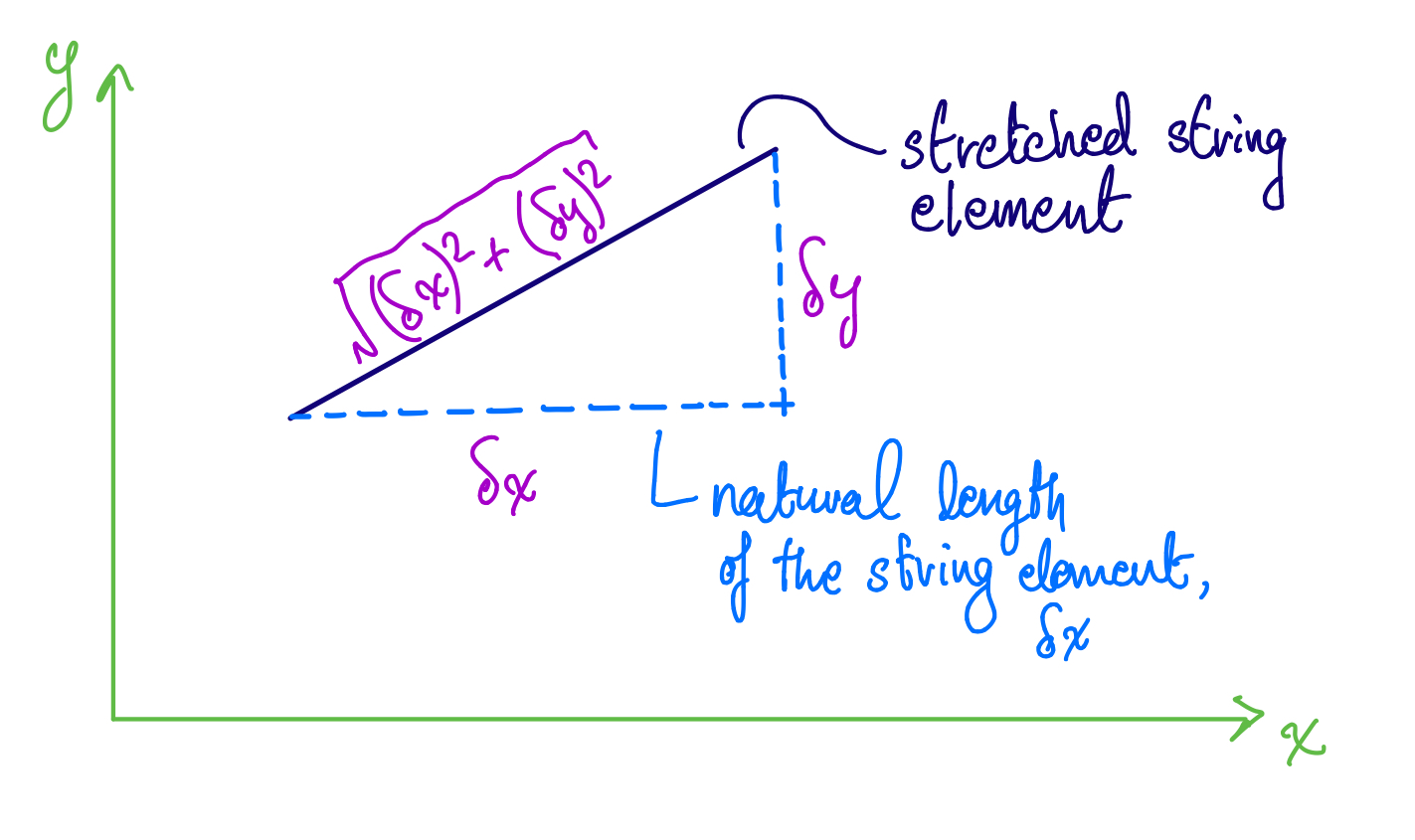
The stretched length of the string element, $(\delta x)'$ is given by $\sqrt{(\delta x)^2 + (\delta y)^2}$, by applying Pythagoras' theroem.
From the diagram above, we can say that the stretched length of the string element is given by:
$$(\delta x)' = \sqrt{(\delta x)^2 + (\delta y)^2} = \delta x \sqrt{1 + (\frac{\delta y}{\delta x})^2}$$
We can apply the binomial theorem here and, by ignoring terms of degree higher than 2, approximate this to:
$$\Rightarrow (\delta x)' \approx \delta x (1 + \frac{1}{2}(\frac{\delta y}{\delta x})^2)$$
This is an important step so if you're not familiar with using the binomial theorem to approximate a square root term, make sure to research that and understand it well.
The extension, $\Delta x$, is given by this expression minus the natural length of the element:
$$\Delta x = (\delta x)' - \delta x = \delta x (1 + \frac{1}{2}(\frac{\delta y}{\delta x})^2) - \delta x $$ $$\Rightarrow \Delta x = \delta x(\frac{1}{2}(\frac{\delta y}{\delta x})^2) = \frac{1}{2} \delta x (\frac{\delta y}{\delta x})^2$$
We can now use the formula above to find the elastic potential energy of the string element:
$$\delta V = T\Delta x$$ $$\Rightarrow \delta V = \frac{1}{2} T \delta x (\frac{\delta y}{\delta x})^2$$
Again dividing by $\delta x$ and taking the limit as it approaches 0:
$$\Rightarrow \frac{\delta V}{\delta x} = \frac{1}{2} T (\frac{\delta y}{\delta x})^2$$ $$\Rightarrow \frac{dV}{dx} = \frac{1}{2} T (\frac{\partial y}{\partial x})^2$$
This is the potential energy density in the string. And we can again integrate with respect to $x$ to obtain the total potential energy in the string:
$$V = \int \frac{1}{2} T (\frac{\partial y}{\partial x})^2 dx = \frac{1}{2} T \int (\frac{\partial y}{\partial x})^2 dx$$
Total energy in the string
We can now add the kinetic and potential energies of the string to obtain an expression for the total energy propagating through the string, $E$:
$$E = K + V$$ $$\Rightarrow E = \frac{1}{2}\rho \int (\frac{\partial y}{\partial t})^2 dx + \frac{1}{2} T \int (\frac{\partial y}{\partial x})^2 dx$$
Recall from Waves II, that the speed of the waves on the string is given by:
$$c = \sqrt{\frac{T}{\rho}} \Rightarrow T = \rho c^2$$
Substituting T in the expression for total energy:
$$E = \frac{1}{2}\rho \int (\frac{\partial y}{\partial t})^2 dx + \frac{1}{2} \rho c^2 \int (\frac{\partial y}{\partial x})^2 dx$$ $$\Rightarrow E = \frac{1}{2}\rho \int((\frac{\partial y}{\partial t})^2 + c^2(\frac{\partial y}{\partial x})^2)dx$$
Again from Waves II, that for a constant-shape travelling wave, we have $y(x,t) = y(x\pm ct)$. We had also found the relation between the first partial derivatives of $y$ with respect to $t$ and $x$ to be:
$$\frac{\partial y}{\partial t} = \pm c\frac{\partial y}{\partial x}$$
Squaring both sides, we get a result that we can use in our expression for energy:
$$(\frac{\partial y}{\partial t})^2 = c^2 (\frac{\partial y}{\partial x})^2$$
Substituting $(\frac{\partial y}{\partial t})^2$ back into our energy expression:
$$E = \rho c^2 \int (\frac{\partial y}{\partial x})^2 dx$$
We could also instead substitute $(\frac{\partial y}{\partial x})^2 = \frac{1}{c^2} (\frac{\partial y}{\partial t})^2$ (don't get confused; this is not the wave equation!) to arrive at an equally valid result:
$$E = \rho \int (\frac{\partial y}{\partial t})^2 dx$$
The next step now is to consider the power being transported by the wave, which we will do in the next post.
Closing Remarks
Thanks for reading! Hopefully you found this post informative and easy to follow.
If there's anything you would like to be clarified or if you have any question or want to discuss something, please feel free to contact me as usual either through the comments below or privately through the website.
Happy Physics-ing!
Update (05/02/2018): Waves IV is now up, here.
Related
You may also be interested in:
Waves II: Wave Speed for Waves on a String