Waves IV: Power transported by a Wave on a String
Posted by Youssef Moawad on: 05/02/2018, in Physics
Intro
In transmission systems, we are often interested in the amount of power that we can transmit given particular conditions. So it would be helpful to derive an expression for the power in terms of the physical conditions of your system. In our case, we will be continuing on our wave on a string discussion, where the physical properties are the tension, $T$, the linear density of the string, $\rho$, and the speed of the waves on the string, $c = \sqrt{\frac{T}{\rho}}$.
The analysis performed here, however, will be applicable to other transmission systems as well. In a later article, we will be considering the case of a power transmission line, for example.
Recap of Energy in a String
This post carries on directly from the previous one, Waves III, where we discussed the kinetic and elastic potential energies propagated by a wave on a string. It's recommended to read that part before continuing on, if you haven't already.
Last time, we derived the following expression for the energy in a wave on a string:
$$E = \frac{1}{2}\rho \int((\frac{\partial y}{\partial t})^2 + c^2(\frac{\partial y}{\partial x})^2)dx$$
We also saw that for a constant-shape travelling wave, this can be expressed in the two equivalent forms:
$$E = \rho c^2 \int (\frac{\partial y}{\partial x})^2 dx = \rho \int (\frac{\partial y}{\partial t})^2 dx$$
In this post, we're going to use these to derive expressions for the energy carried by one cycle of the wave (average over one wavelength) as well as the power passing a point on the string.
Average energy carried by one cycle
Consider a simple constant-shape travelling wave that has the form:
$$y(x,t) = A\sin(kx - \omega t)$$
where $A$ is the amplitude of the wave, $\omega = 2\pi f$ is the angular velocity and $k = \frac{2\pi}{\lambda}$ is the wave number of the wave. It is important to note that:
$$c = f\lambda = \frac{\omega}{k}$$
We can take a wave of any constant-shape form and apply the same analysis we're going to do and get similar results. I leave it up to you to verify that this solution satifies the wave equation derived in Waves I (do this by taking the second partial derivatives of $y$ with respect to $x$ and $t$, substitute into the wave equation and verify that the value that $c$ needs to be is $\frac{\omega}{k}$).
We need to use this in the expression we derived in the last post. So let's take the first derivative with respect to $x$ and square it:
$$\frac{\partial y}{\partial x} = Ak\cos(kx - \omega t)$$ $$\Rightarrow (\frac{\partial y}{\partial x})^2 = A^2k^2\cos^2(kx - \omega t)$$
Side note: Average value of $\cos^2(x)$ and $\sin^2(x)$
Since we're interested in finding the average value of the energy propagated by one cycle, we need to know the average values of $\cos^2(x)$ and $\sin^2(x)$. We can plot these functions and see that they are symmetric about the line $y=\frac{1}{2}$ and hence we can say that
$$\overline{\cos^2(x)} = \overline{\sin^2(x)} = \frac{1}{2}$$
We can see this better when we visualise it:
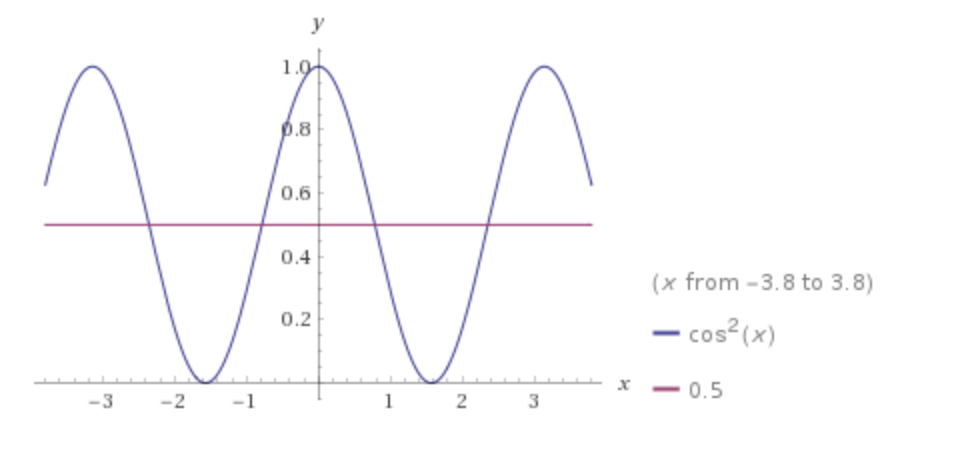
Plot of $cos^2(x)$. It can be seen that, through one wavelength, the function's average value is 0.5.
Plot from WolframAlpha
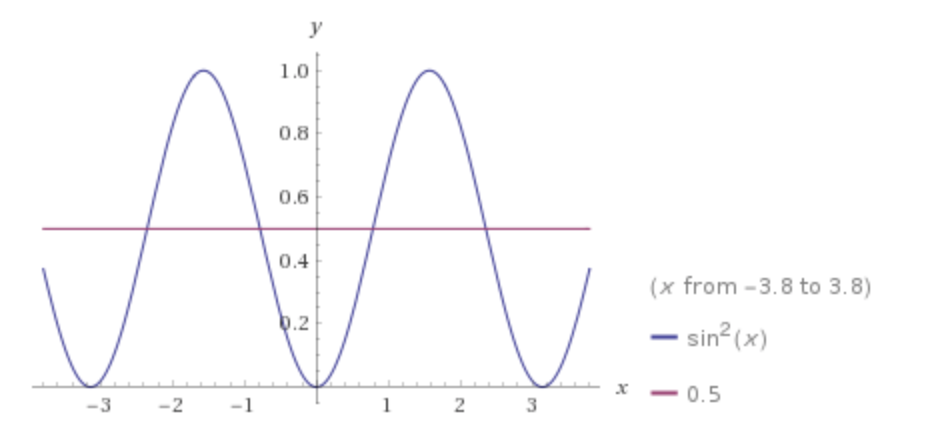
Plot of $sin^2(x)$. Similar to the above plot, we can see that, through one wavelength, the function's average value is 0.5.
Plot from WolframAlpha
Let's now substitute this into our expression for energy and apply integration limits across one wavelength:
$$E_{onecycle} = \rho c^2 \int _{one \lambda} (\frac{\partial y}{\partial x})^2 dx$$ $$\Rightarrow E_{onecycle} = \rho c^2 \int _{one \lambda} A^2k^2\cos^2(kx - \omega t) dx$$
Because we're interested in the average value of this across one wavelength, we can replace the cosine term with $\frac{1}{2}$ as described in the side note, and get:
$$\Rightarrow E_{onecycle} = \frac{1}{2} \rho A^2k^2c^2 \int _{one \lambda} dx$$
The integral here is equivalent to the wavelength of the wave, $\lambda$. So we can write:
$$\Rightarrow E_{onecycle} = \frac{1}{2} \rho A^2k^2c^2\lambda$$
Now note that because $c=\frac{\omega}{k}$, it's implied that $\omega^2 = c^2k^2$. So we can say:
$$\Rightarrow E_{onecycle} = \frac{1}{2} \rho A^2\omega^2\lambda$$
This is the energy propagated by the wave over one wavelength. Note that it is constant with respect to time and only relates to the parameters of the wave, $\omega$, $\lambda$ and $A$, and the physical properties of the string, $\rho$.
Feel free to apply similar analysis starting from a solution of the form $y(x,t) = A\cos(kx - \omega t)$ and see that you arrive at a similar result.
Power
We can now use this expression to derive the power passing a point on the string. Since this is the energy propagated on one wavelength, and one wavelength take a constant period of time, $T = \frac{1}{f}$, to pass a point on the string (basics of waves), we can simply divide through by the period to obtain the power:
$$P = \frac{E_{onecycle}}{T} = E_{onecycle}f = \frac{1}{2} \rho A^2\omega^2\lambda f$$
Now, recall that $c = f\lambda = \sqrt{\frac{T}{\rho}}$. So we can write the above expression as:
$$\Rightarrow P = \frac{1}{2} \rho A^2\omega^2 c = \frac{1}{2} \rho A^2\omega^2\sqrt{\frac{T}{\rho}}$$
And finally, we can say that:
$$P = \frac{1}{2} A^2\omega^2\sqrt{T\rho}$$
As discussed above, this expression of the power only depends on the physical properties of the string and the wave, and is constant with time.
Closing Remarks
I hope you found this post helpful and informative.
In the next post, we will start discussing the impedance of the string. So stay tuned for that!
As usual, any feedback is appreciated and feel free to send me any questions or comments you have, either through the comments below or you can contact me through the website.
Happy Physics-ing!
Update (13/02/2018): Waves V is now up, here.
Related
You may also be interested in:
Waves III: Energy Propagated by a String