A Brief Post

Welcome back to another post about the Maxwell Relations. This will be a brief post where I will present a very useful mnemonic for remembering the Maxwell Relations that certainly proved quite helpful during my studies of thermodynamics.

This post follows directly (but will be much less mathematical) from the previous post, where I derived the Maxwell Relations.

Recap

As a quick recap; the Maxwell Relations are a set of relationships between the partial derivatives of the intensive and extensive properties of a thermodynamic system which are quite useful because they allow us to change certain quantities, that are often difficult to measure, to others which are more readily measured.

The Maxwell Relations we derived are:

$$ (\frac{\partial T}{\partial V})_S = -(\frac{\partial P}{\partial S})_V $$ $$ (\frac{\partial T}{\partial P})_S = (\frac{\partial V}{\partial S})_P $$ $$ (\frac{\partial P}{\partial T})_V = (\frac{\partial S}{\partial V})_T $$ $$ (\frac{\partial V}{\partial T})_P = -(\frac{\partial S}{\partial P})_T $$

where $T$ is temperature, $V$ is volume, $S$ is entropy and $P$ is pressure. Also the notation $(\frac{\partial T}{\partial V})_S$ means the partial derivative of $T$ with respect to $V$ while keeping $S$ explicitly constant. This is known as constrained variable notation.

It might also be useful to recall the four thermodynamic potentials we discussed last time and their natural variables:

Thermodynamic Potential	Differential Form	Natural Variables
Internal Energy, $U$	$dU = TdS - PdV$	$S$, $V$
Enthalpy, $H$	$dH = TdS + VdP$	$S$, $P$
Helmholtz Free Energy, $F$	$dF = -PdV - SdT$	$V$, $T$
Gibbs Free Energy, $G$	$dG = VdP - SdT$	$P$, $T$

The Mnemonic

The key to this mnemonic is the phrase Good Physicists Have Studied Under Very Fine Teachers. Notice how the first letter of every word can represent a thermodynamic potential or variable:

Good - Gibbs Free Energy
Physicists - Pressure
Have - Enthalpy
Studied - Entropy
Under - Internal Energy
Very - Volume
Fine - Helmholtz Free Energy
Teachers - Temperature

We can use this to write out a thermodynamic square, where thermodynamic potentials go on the sides of the square and other variables go on the corners, in a counter-clockwise fashion:

Thermodynamic square formed by adding the letters from the mnemonic on the sides and corners of the square starting at the right hand side and moving counter-clockwise.

Cleaning this up by removing the words and the green arrows along with the square:

Thermodynamic square showing the variables and thermodynamic potentials.

Deducing natural variables of thermodynamic potentials

Notice how in the above square each thermodynamic potential has its natural variables around it. For instance, the Gibbs Free Energy, $G$, has pressure, $P$, above it and temperature, $T$, underneath it. We can also extend this to the rest of the potentials:

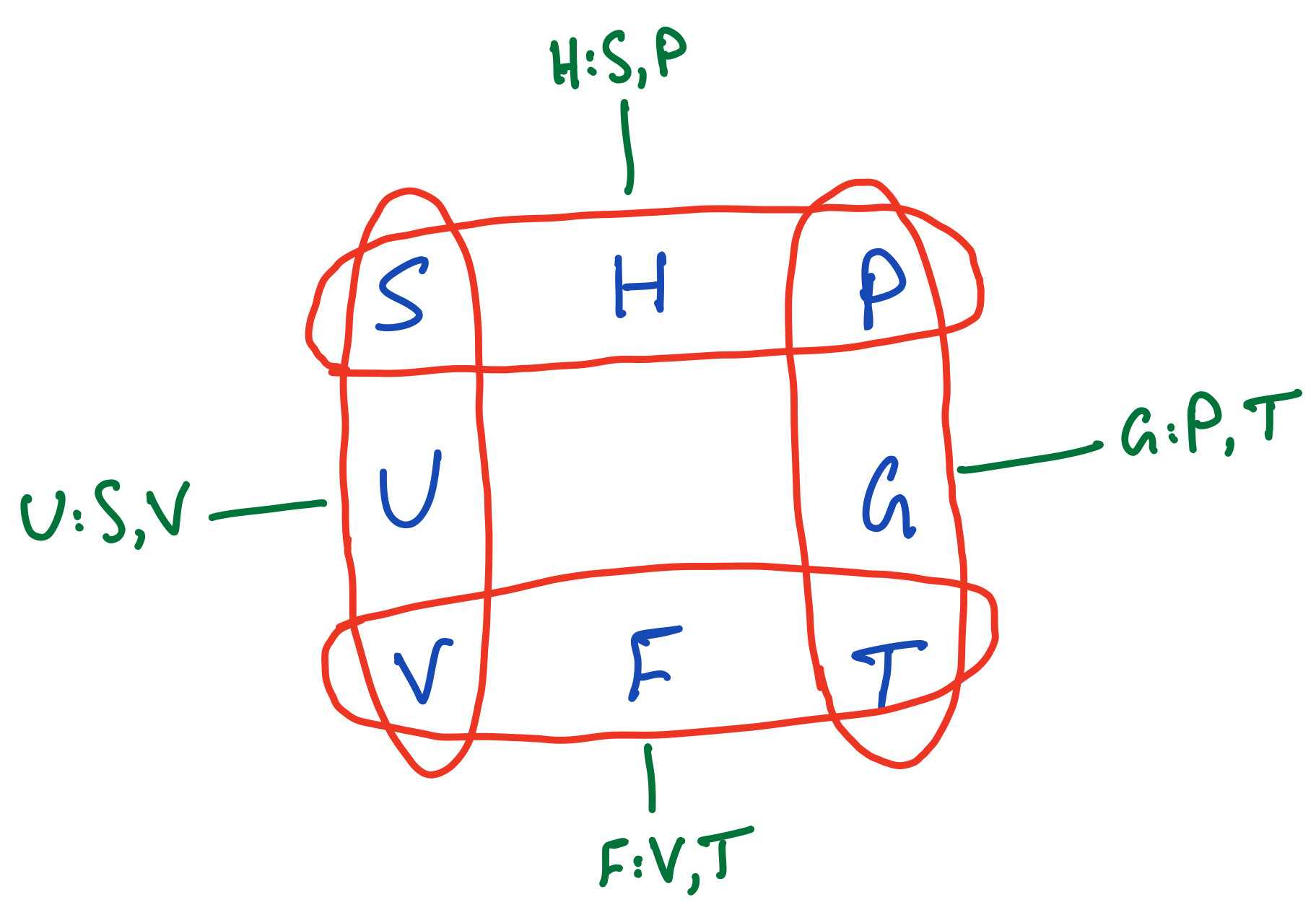
Deducing the natural variables of thermodynamic potentials from the thermodynamic square.

Deducing Maxwell's Relations

Let us now simplify the square further by removing the thermodynamic potentials and having only the variables $P$, $S$, $V$ and $T$ on the square, still in the same locations:

Thermodynamic square leaving out the potentials.

In order to get the Maxwell relations from this square, we start to draw pairs of arrows going on the diagonals between the variables. We draw two arrows at a time, each arrow representing a partial differential expression (one of those involved in a Maxwell Relation). An upwards looking arrow represents a positive quantity while a downwards looking one represents a negative quantity. The beginning of an arrow represents the variable being differentiated and the end of an arrow represents the variable being held explicitly constant. The variable against which differentiation is happening is the one at the end of the other arrow. Take care so as to not get confused here!

For instance, the first Maxwell relation can be deduced by drawing an arrow from $P$ to $V$ and an arrow from $T$ to $S$:

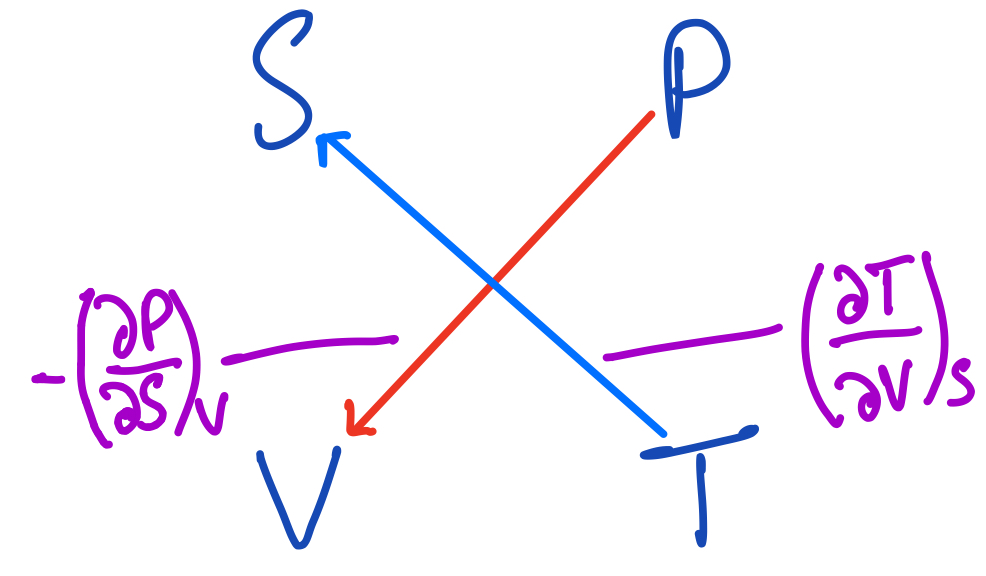
The first Maxwell Relation using the thermodynamic square.

The arrow from $P$ to $V$ says to differentiate $P$ while keep $V$ explicitly constant, but since it's going downwards, give it a negative sign. The other arrow gives the variable against which to differentiate $P$, $S$. It also says to differentiate $T$ while keeping $S$ constant and the first arrow again says to differentiate $T$ with respect to $V$.

Equating the expressions these arrows represent, we get the first Maxwell Relation:

$$ (\frac{\partial T}{\partial V})_S = -(\frac{\partial P}{\partial S})_V $$

We can now apply the same strategy while drawing other arrows. Before we go on to do this, I encourage the reader to try this out themselves and see if they can deduce the other Maxwell Relations from this square, without reading ahead.

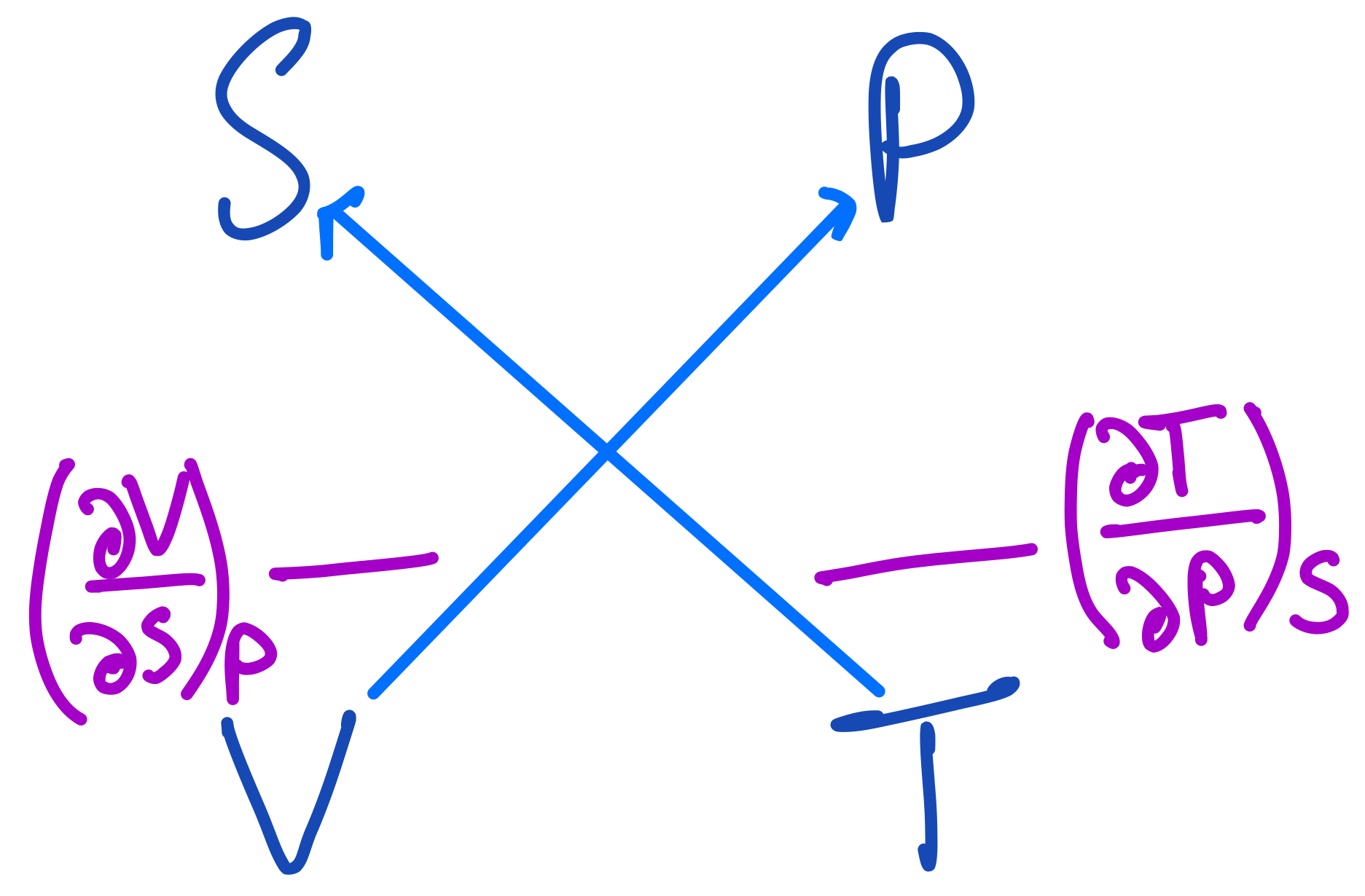
The second Maxwell Relation from the thermodynamic square.

From this we get the second relation:

$$ (\frac{\partial V}{\partial S})_P = -(\frac{\partial T}{\partial P})_S $$

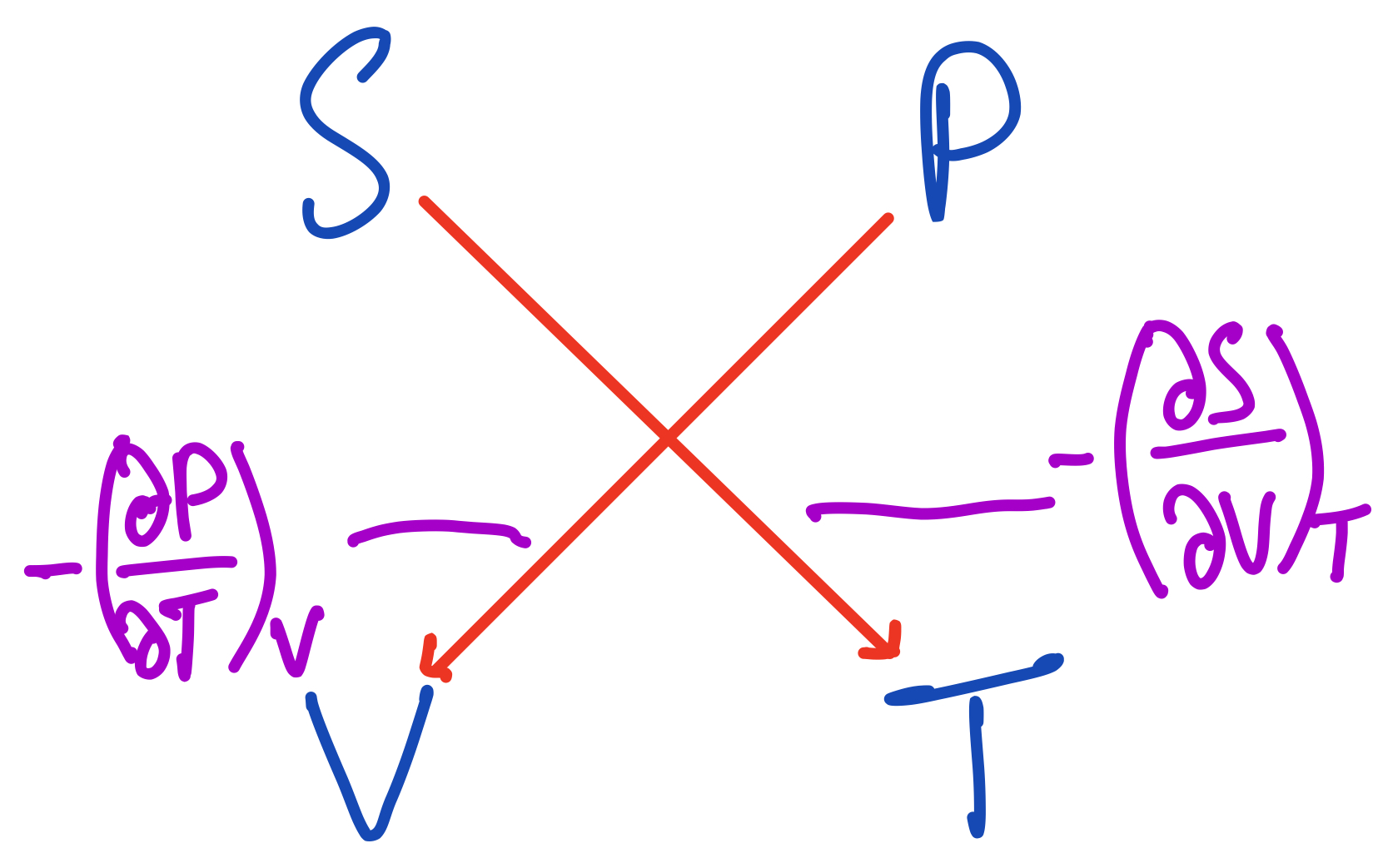
The third Maxwell Relation from the thermodynamic square.

From these arrows, we get this relation:

$$ -(\frac{\partial P}{\partial T})_V = -(\frac{\partial S}{\partial V})_T $$

Since there's a minus sign on both sides, we can cancel them out and get the relation we're more familiar with:

$$ (\frac{\partial P}{\partial T})_V = (\frac{\partial S}{\partial V})_T $$

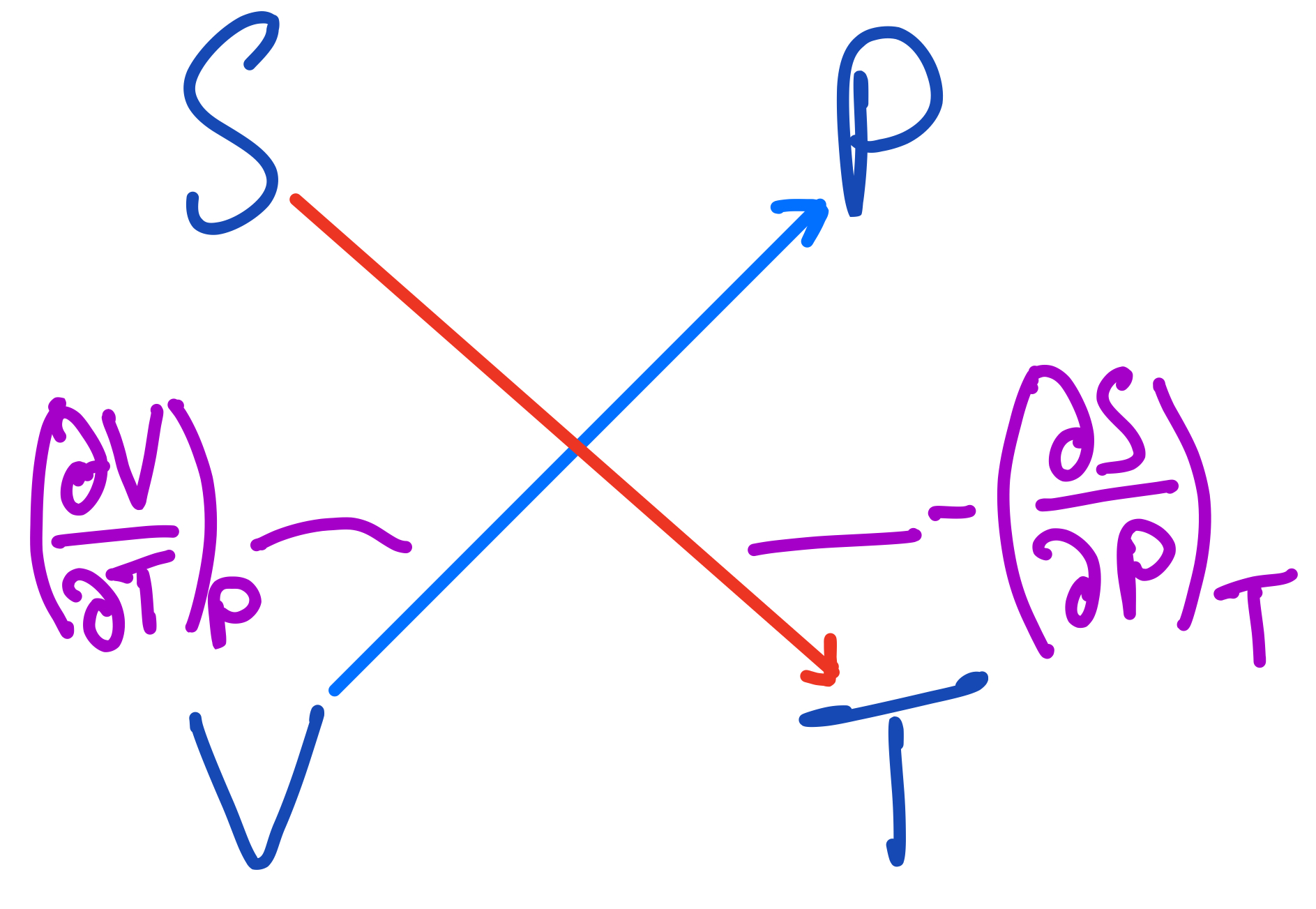
The fourth Maxwell Relation from the thermodynamic square.

And finally, the last relation is:

$$ (\frac{\partial V}{\partial T})_P = -(\frac{\partial S}{\partial P})_T $$

Conclusions

In this post, we managed to deduce the four Maxwell Relations we derived in the previous post using the mnemonic we introduced. Remember, the key is the phrase Good Physicists Have Studied Under Very Fine Teachers.

We also saw how we can find the natural variables of each of the four thermodynamic potentials we discussed previously using this mnemonic, which can be fairly handy sometimes.

What's Next

I recently started a new series on the blog about digital circuits, which I've been learning about in my free time the past while. Feel free to check that out, if you're interested. I've only written the first part at this point and there's more planned. Find the first part here.

There's also more thermodynamics blogs coming though! Currently planned are ones about using the Maxwell Relations to derive relationships between the heat capacities as well as an introduction to statistical mechanics and the partition function.

Closing remarks

Thanks for reading! I hope you've found the article helpful. As usual, feedback is very much appreciated and will go towards improving the blog. So feel free to leave a comment below, contact me through the website, or tweet me @_devdude.

Happy Physics-ing!