Let's go on!

In the first part of this series, I introduced the Standard Model and gave a brief introduction about fermions, which are the particles that make up everything we can see, and bosons, which are the particles that mediate the fundamantal forces between these particles.

In most early particle physics courses, students are introduced to the idea of particle interactions and are taught about the various quantities, that may be conserved (or not conserved), that are involved. These quantities are the quantum numbers, which we have discussed before. On a personal note, this was one of the topics that most interested me about particle physics during university. The conservation of these quantum numbers between the start and the end of interaction (and in the vertices of the Feynman Diagrams, as we'll see later) and the symmetries surrounding these phenomena was very appealing to me. Indeed, it inspired me to start working on a mobile app, The Standard Model, that lets users manipulate particles, check interactions and have Feynman Diagrams drawn for them for these interactions.

Let's get started then! I hope you find this article informative and entertaining.

If you have not come across Feynman diagrams before, it is highly recommended that you read the prelude article to this part: Visualising Interactions with Feynman Diagrams. I will assume that you know about everything I covered in that post.

A quick change in terminology

Indeed, a better term by which to refer to these forces would be fundamental interactions, and we shall refer to them as such going forward. An interaction here might be a decay of a particle or a collision of two or more particles for instance. These interactions refer to the same thing as the fundamental forces and to each corresponds a boson as we'll see in the following sections.

The Standard Model: Revisited

Because we'll be discussing particle interactions in the context of the Standard Model of particle physics, I think we should have a brief overview of what's involved.

The Standard Model of particle physics.

Image from Wikipedia

Quarks

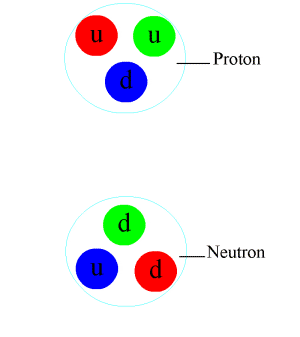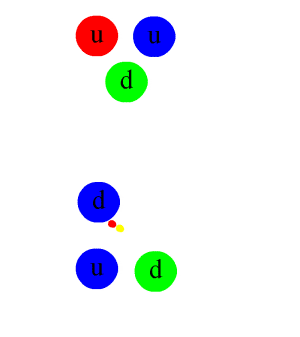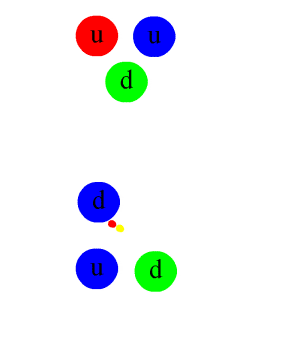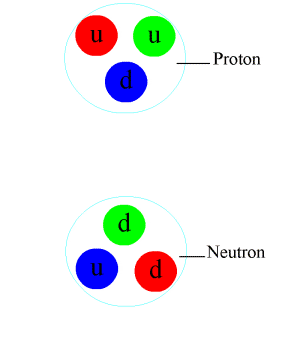
Quarks are the particles that make up baryons (which are combinations of three quarks/antiquarks, e.g. protons and neutrons) and mesons (which are combinations of a quark and an antiquark). Quarks carry an electric charge (a multiple of 1/3), a colour charge (one of red, green, blue or a corresponding anticolour) and a quark flavour (depending on the type of quark). Quarks also carry a baryon number of 1/3 or -1/3 such that when three quarks/antiquarks combine to form a baryon, the total baryon number is either +1 or -1. The six quarks and their flavours and charge are summarised in this table:

	Symbol	Upness	Downness	Charm	Strangeness	Topness	Bottomness	Charge
Up Quark	u	1	0	0	0	0	0	2/3
Down Quark	d	0	1	0	0	0	0	-1/3
Charm Quark	c	0	0	1	0	0	0	2/3
Strange Quark	s	0	0	0	-1	0	0	-1/3
Top Quark	t	0	0	0	0	1	0	2/3
Bottom Quark	b	0	0	0	0	0	1	-1/3

The quarks are confined in baryons and mesons by means of a phenomenon called quark confinement and involving gluon exchange. These phenomena occur due to the strong interaction and the colour charge of the quarks and are explained by the theory of Quantum Chromodynamics. I have explained these in part 2 of this series: Colourful Quantum Chromodynamics, and as such I will most likely not be going into the strong nuclear interaction in too much detail in this article.

Leptons

Leptons are defined as the fermions which do not take part in the strong interaction (unlike quarks, which do). The most notable lepton is the familiar electron. Other leptons include the muon, the tau and a neutrino corresponding to each one of those. The non-neutrino leptons carry an electric charge and all the leptons carry a lepton number. These properties are summarised here:

	Symbol	Electron Lepton Number	Muon Lepton Number	Tau Lepton Number	Charge
Electron	e-	1	0	0	-1
Electron Neutrino	νe	1	0	0	0
Muon	μ-	0	1	0	-1
Muon Neutrino	νμ	0	1	0	0
Tau	τ-	0	0	1	-1
Tau Neutrino	ντ	0	0	1	0

Bosons

Bosons are the particles that come into play when an interaction is taking place. They mediate the interaction. Each boson corresponds to a particular fundamental interaction. The bosons will be described in detail in the coming sections as we consider each interaction in detail.

Interactions

So an interaction occuring for one or more particles is simply one of the four fundamental forces acting. So it makes sense that each interaction has the same boson as the corresponding force. The interactions and their bosons are given in this table:

Interaction	Boson(s), or mediator	Description
Electromagnetic Interaction	Photon (γ)	The electromagnetic interaction is responsible for phenomena involving electrically charged particles (for example, the photoelectric effect).
Strong Nuclear Interaction	Gluon (g), mesons	The strong nuclear interaction is responsible for phenomena involving colour charged particles (mainly quarks and gluons). Mainly it works to keep quarks confined inside hadrons (like protons and neutrons) and to keep atomic nuclei intact.
Weak Nuclear Interaction	W+, W-, Z0	The weak nuclear interaction is mainly responsible for radioactive decay, the most common example of which is beta decay, by which a neutron releases an electron and a neutrino and becomes a proton. It acts such that it changes the quark flavour of the involved particles.
Gravitation	Graviton (hypothesised)	As the Standard Model does not (yet) incorporate a theory of gravity, there is not much to be said about the gravitational interaction in this context.

These interactions must conserve certain quantities including the quantum numbers associated with the involved particles (charge, quark flavour, lepton number, baryon number, etc.) as well as momentum and energy. For the purpose of this article, we will mainly consider the conservation of these quantum numbers. If you would like to read more about conservation laws, check out Symmetries: The Beauty in Physics.

We will now consider each of the interactions (bar gravity as a theory of gravity is not included in the Standard Model), discuss it in further detail and give some examples, along with Feynman diagrams, about how it takes place.

Regarding Mass and Energy

When I give examples of specific interactions below, I will often refer to energy needing to be equivalent to the rest mass of a particle. How can this be? E = mc²! One of the most important results from Special Relativity is mass-energy equivalency and this means that the energy of a system is numerically equal to the mass of its components multiplied by the speed of light squared.

It is important to keep in mind that we cannot talk about "converting" mass into energy, because they are indeed manifestations of the same thing. A system with a higher internal energy will have an ever so slightly higher mass.

I will most likely be writing an article in the future regarding mass-energy equivalency to discuss this further.

Massless Particles

It is also important to realise that some particles in the Standard Model (namely the photon and the gluon) are massless. This does not mean that they have no energy as they still have an associated energy that is related to their momentum, which, in turn, is related to their de Broglie wavelength. I have discussed this de Broglie wavelength briefly in my article about the double slit experiment, but this also has another very important result, namely wave-particle duality.

I digress however! An important property of massless particles, that you should keep in mind, is that they always travel at the speed of light in a vacuum. This should not come as a surprise because you know that the photon is the particle that makes up light, so it makes sense that it moves with the same speed!

The Electromagnetic Interaction

The electromagnetic interaction acts between all charged particles (so this includes all the fermions except for the neutrinos). It is mediated by the photon, which is a massless uncharged particle. You will also be familiar with the photon as the particle that makes up light. This makes sense because light is essentially just an electromagnetic disturbance, i.e. an electric field moving perpendicular to a magnetic field (there is more to be said about this but it goes beyond our scope).

The electromagnetic interaction causes most forces we experience between everyday objects. When you push a box, for instance, the electromagnetic interaction acts such that your hand does not go through the box, and the box actually experiences a pushing force and moves. It also ultimately determines the properties of the elements and chemical bonding.

Because the photon is massless, the range of the electromagnetic interaction is infinite and so any two charges separated by any distance will experience some force between them. The strength of the interaction drops as the distance squared between the charges increases, obeying the inverse square law. The distance squared between the charges increases rapidly as the distance between the charges increases. So two charges separated by a very large distance will in fact experience an electromagnetic force, however it will be very minute. This arises from Coulomb's law:

$$F=-\frac{q_1q_2}{4\pi\varepsilon_0r^2}$$

Coulomb's law describing the force experienced by two charges, $q_1$ and $q_2$, separated by a distance $r$.

Because I do not aim to fully introduce mathematical concepts in these articles (for the time being at least), you do not need to be able to completely understand this equation and it is only included here for completion. It is only important to appreciate that the strength of the electromagnetic interaction decreases as the square of the distance between the charges increases, as mentioned above.

Electromagnetic interactions in the quantum world

We have deviated slightly from particle physics as the law shown above can be applied to any two charged objects and is mainly concerned with electrostatics. Let's circle back to quantum particles and discuss some examples of electromagnetic interactions on a particle scale.

Pair annihilation

You may or you may not know that when matter comes in contact with antimatter, they both annihilate and energy is released. This energy comes from their rest masses and their kinetic energies. In particle physics, this energy manifests as a photon. For instance an electron coming in contact with a positron (an antielectron) will cause both of them to annihilate releasing a photon.

$$e^-+\;e^+\xrightarrow{}\;\gamma$$

An electron and a positron coming in contact, annihilating and releasing a photon that has energy equivalent to their rest masses and their kinetic energy.

If you have read Symmetries: The Beauty in Physics, you will know that certain quantities here need to be conserved so let's have a look at that. We know that the electron has an electron lepton number and a charge which need to be conserved here. The electron lepton number of the electron is +1 and its charge is -1. Because the positron is the electron's antiparticle, it has an electron lepton number of -1 and a charge of +1. So indeed, if we consider the "reactant" side of the interaction, the total electron lepton number and the total charge are both 0. This makes sense because if we look at the "products" side of the interaction, we have just the photon, which we know to be uncharged and to have an electron lepton number of 0 (because only leptons have any lepton number).

Below, you can see the Feynman diagram for this interaction. You should be able to show that conservation laws are obeyed before and after the vertex.

Feynman diagram showing an electron and a positron colliding, annihilating and forming a photon. Notice that because the positron is an antiparticle, it has an arrow pointing backwards. You should try to distinguish between particles and antiparticles in this way, in addition to their labels, in the examples to come.

This interaction can also happen for any particle-antiparticle pair that can interact electromagnetically. Here are some examples involving muons and quarks:

$$\mu^-+\;\mu^+\xrightarrow{}\;\gamma$$ $$u\;+\;\overline u\xrightarrow{}\;\gamma$$ $$t\;+\;\overline t\xrightarrow{}\;\gamma$$ $$c\;+\;\overline c\xrightarrow{}\;\gamma$$

Examples of more particles and antiparticles annihilating releasing a photon. See if you can show indeed that conservation laws are obeyed for each interaction. Hint: the first involves muon lepton number, and the rest involve quark flavour numbers (upness, downness, etc.).

The Feynman diagrams for these interactions would be equivalent to the Feynman diagram shown above but with a different particle-antiparticle pair. Indeed, we can draw this as a general Feynman diagram for pair annihilation:

Feynman diagram showing general pair annihilation. Keep in mind that the particles represented by p need to be able to interact electromagnetically, i.e. have electric charge.

Pair production

In contrast to how a particle can meet its antiparticle and annihilate forming a photon, a photon can spontaneously decay into a particle-antiparticle pair in a process called pair production. For instance a photon with appropriate energy can decay into an electron and a positron. Energy needs to be conserved of course, so the energy of the photon must at least be greater than the rest masses of the resulting particles. Since this is essentially is the reverse interaction to pair annihilation, it is easy to see how the quantum numbers are conserved so here are some examples starting with electron-positron production:

$\gamma \stackrel{}{\to } e^{-}+ e^{+}$

$\gamma \stackrel{}{\to } d + \overline{d}$

$\gamma \stackrel{}{\to } s + \overline{s}$

$\gamma \stackrel{}{\to } b + \overline{b}$

Examples of pair production. Again, see if you can show that the conservation laws are obeyed.

The generalised Feynman diagram for these interactions will look just the opposite of the Feynman diagram for pair annihilation as you may have guessed:

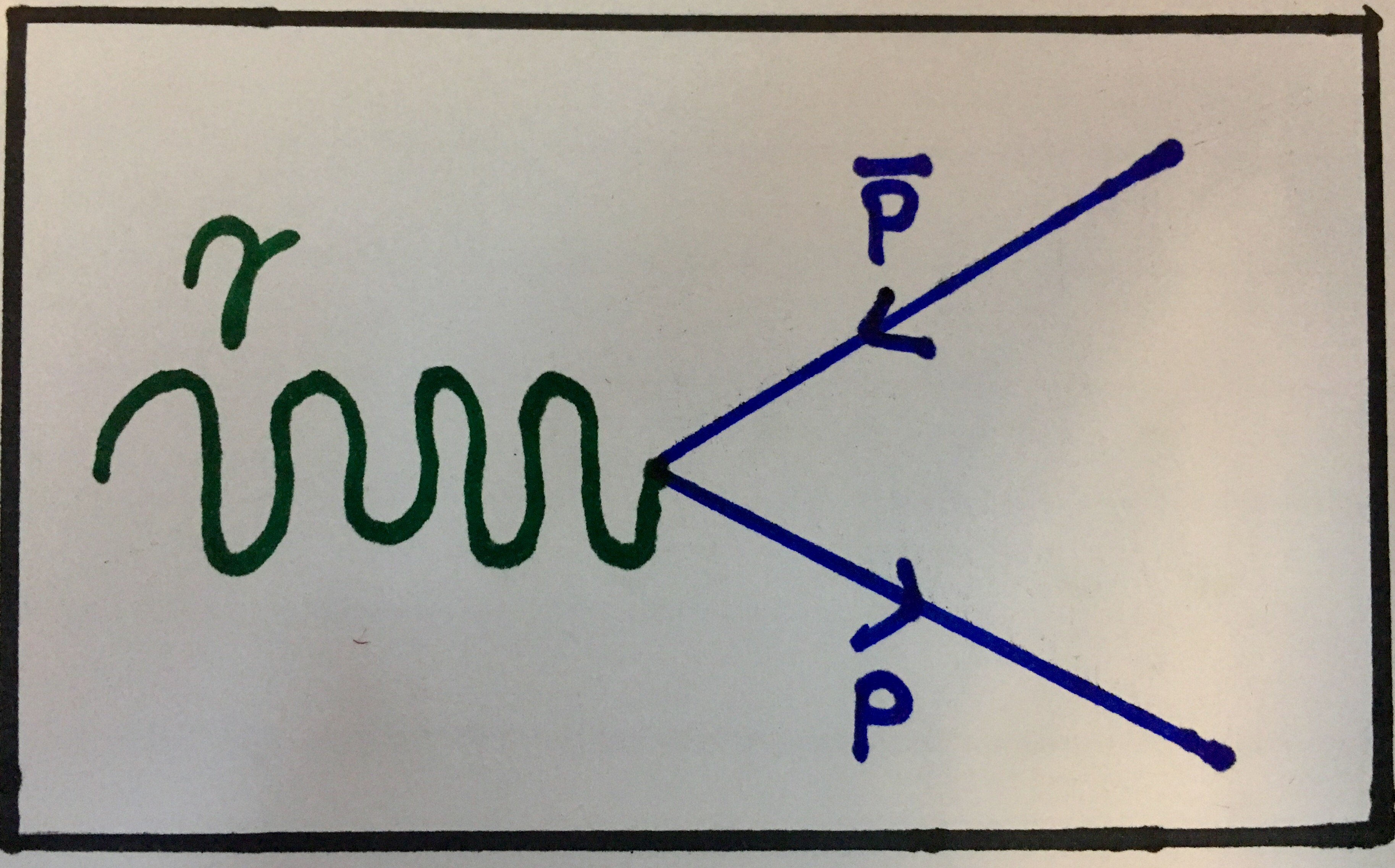
Feynman diagram showing general pair production. Again, the particles produced need to have electric charge as this is an electromagnetic interaction.

Combining pair annihilation and pair production

These two types of interactions (pair annihilation and pair productions) often combine such that a particle-antiparticle pair annihilates forming a photon which then decays into a another particle-antiparticle pair, possibly of a different type. So for instance we can theoretically have interactions that look like this:

$u + \overline{u}\stackrel{}{\to } e^{-}+ e^{+}$

$e^{-}+ e^{+}\stackrel{}{\to } {\mu }^{-}+ {\mu }^{+}$

The first interaction shows an up quark and anti up quark annihilating into a photon (not shown) which then pair produces an electron and a positron. The second interaction shows an electron-positron pair annihilating with the resulting photon then pair producing a muon-antimuon pair.

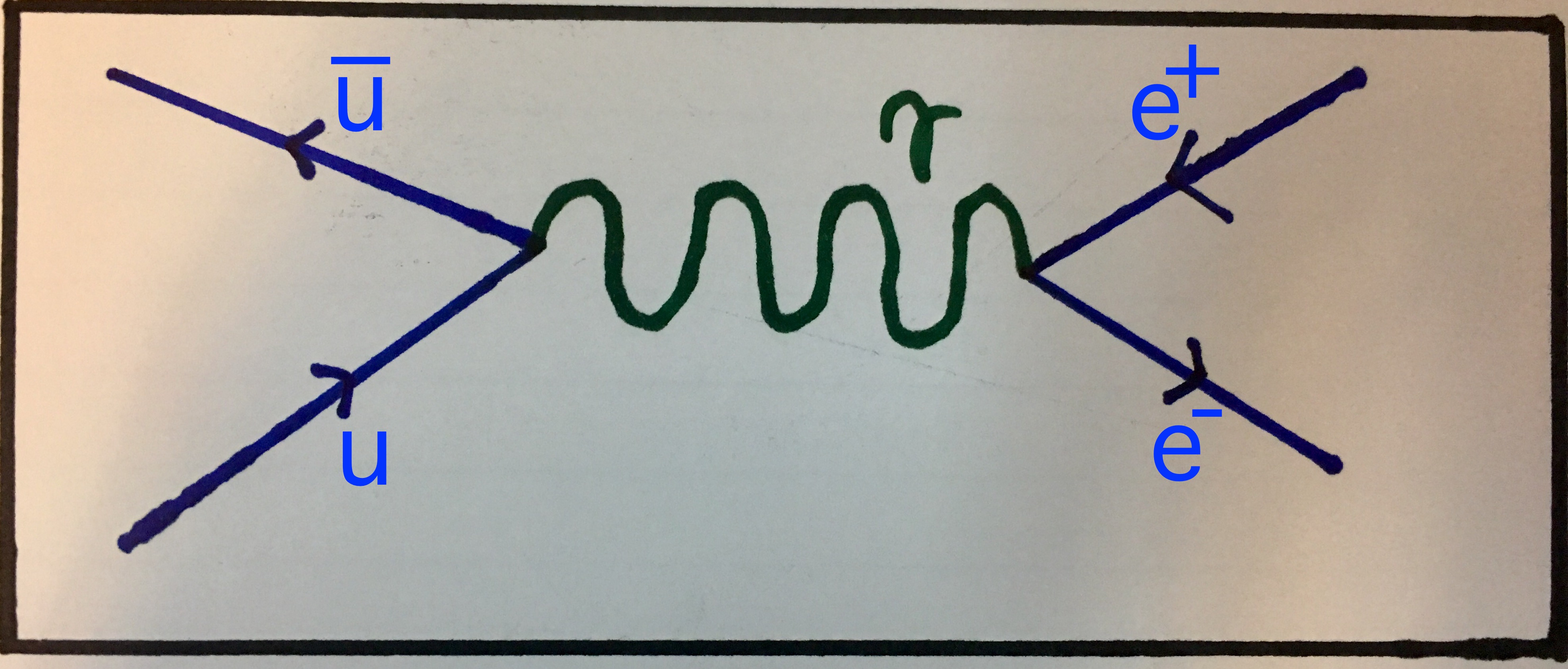
Feynman diagram showing an up quark and an antiup quark pair annihilating into a photon which then pair produces an electron-positron pair.

Similar to the previous image, this Feynman diagram shows an electron and a positron pair annihilating into a photon which then pair produces a muon-antimuon pair.

Electron scattering

This is an interaction fairly different than the ones considered above as it does not involve any particles being annihilated or produced. There are many types of electron scattering but we will consider a very simple case where two electrons are moving towards each other, and deflect. It is easy to understand why this would happen; both electrons are negatively charged and we know that like-charges repel. In particle physics, what happens is that once they reach the distance at which they would deflect, a virtual photon is exchanged between them. There's plenty to be said about virtual particles, but suffice it to say that they are not actually particles at all! They are representations of disruptions in the field responsible for the interaction, in this case, the electromagnetic field. I only mention it because we will see this virtual photon represented in the Feynman Diagram of this interaction later on.

Since the input particles are, simply, two electrons and the output particles are also two electrons, we can represent this interaction in the notation with which we are familiar, like so:

$e^{-}+ e^{-}\stackrel{}{\to } e^{-}+ e^{-}$

Electron scattering. Notice how the input particles represented here are the same as the output particles.

The Feynman diagram for this interaction is fairly simple as it really just is two electrons approaching each other, exchanging a virtual photon then deflecting off of each other, as shown here:

Feynman diagram showing two electrons approaching each other, exchanging a virtual photon and, finally, scattering off in different directions.

Image from Wikipedia

Important note regarding Feynman diagrams

There is often more than one Feynman diagram to represent the same process. These represent different paths that the particles could take to reach the end state and they often have more vertices in them. These are often called higher-order Feynman diagrams and we will not be considering them in this article as we'll always discuss the simplest case.

The Strong Nuclear Interaction

I have discussed the theory of Quantum Chromodynamics before in the last part of this series so I thought for this I would talk about the two acting types of the strong interaction and then give some examples about the strong interaction at work. These two types are the fundamental strong interaction and the residual strong interaction. We will now consider each of these interactions briefly.

The Fundamental Strong Interaction

This is possibly the most important interaction there is and despite this, we never really experience its effect in daily life. The fundamental strong interaction is the one responsible for quarks being confined (held together) inside of hadrons (baryons, like the proton and neutron, and mesons). Quarks are confined through a process called gluon exchange where the quarks exchange colour-carrying gluons to constantly change their colour charges and maintain the bond between them.

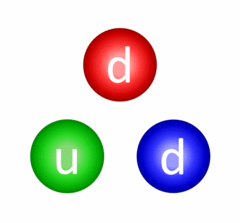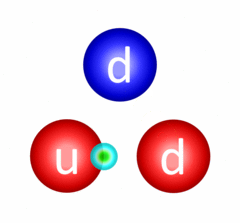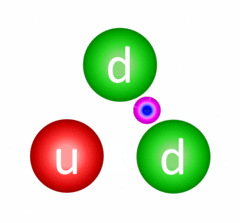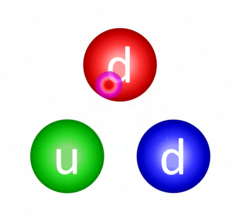
Continuous gluon exchange resulting in quark confinement in a neutron.

Image from Wikipedia

Briefly, this occurs because gluons can be in states where they carry two separate colour charges (a colour and an anticolour of another kind). This gluon is "emitted" by one of the quarks, which changes its colour, and it moves towards another quark, gets absorbed by it and changes the quark's colour. Indeed, the gluons involved in these kinds of interactions are also virtual particles much like the photon described about in electron scattering.

Range

A quick note on the range of this force. Theoretically, the gluon has zero mass and as such we would expect it to move at the speed of light making the range of the fundamental strong interaction infinite. However, this is not the case! If it were, we might feel the effects of the strong force in daily applications. Explanation: Unlike photons, which do not carry electric charge (the charge of the electromagnetic interaction), gluons do carry colour charge (the charge of the strong interaction). This means that gluons interact with each other, whereas photons do not. Essentially, the gluon states that mediate the strong force here move as lumps, which do have mass and as such the strong force has a limited range.

Example

An example of a fundamental strong interaction occuring would be the exchange of a red-antiblue gluon between a red quark and a blue quark. We have considered this example before and we know that the result is that the red quark becomes a blue quark and, in turn, the blue quark becomes a red quark, thus conserving colour charge. We may represent such an interaction like this:

$q_r+q_b\stackrel{g_{r,\overline{b}}}{\to }{q}_b+q_r$

A red and a blue quark interacting to exchange colours.

You have already seen the Feynman diagram for this interaction involving blue and green quarks (in the prelude article) and so here you can see the Feynman diagram for gluon exchange involving red and blue quarks:

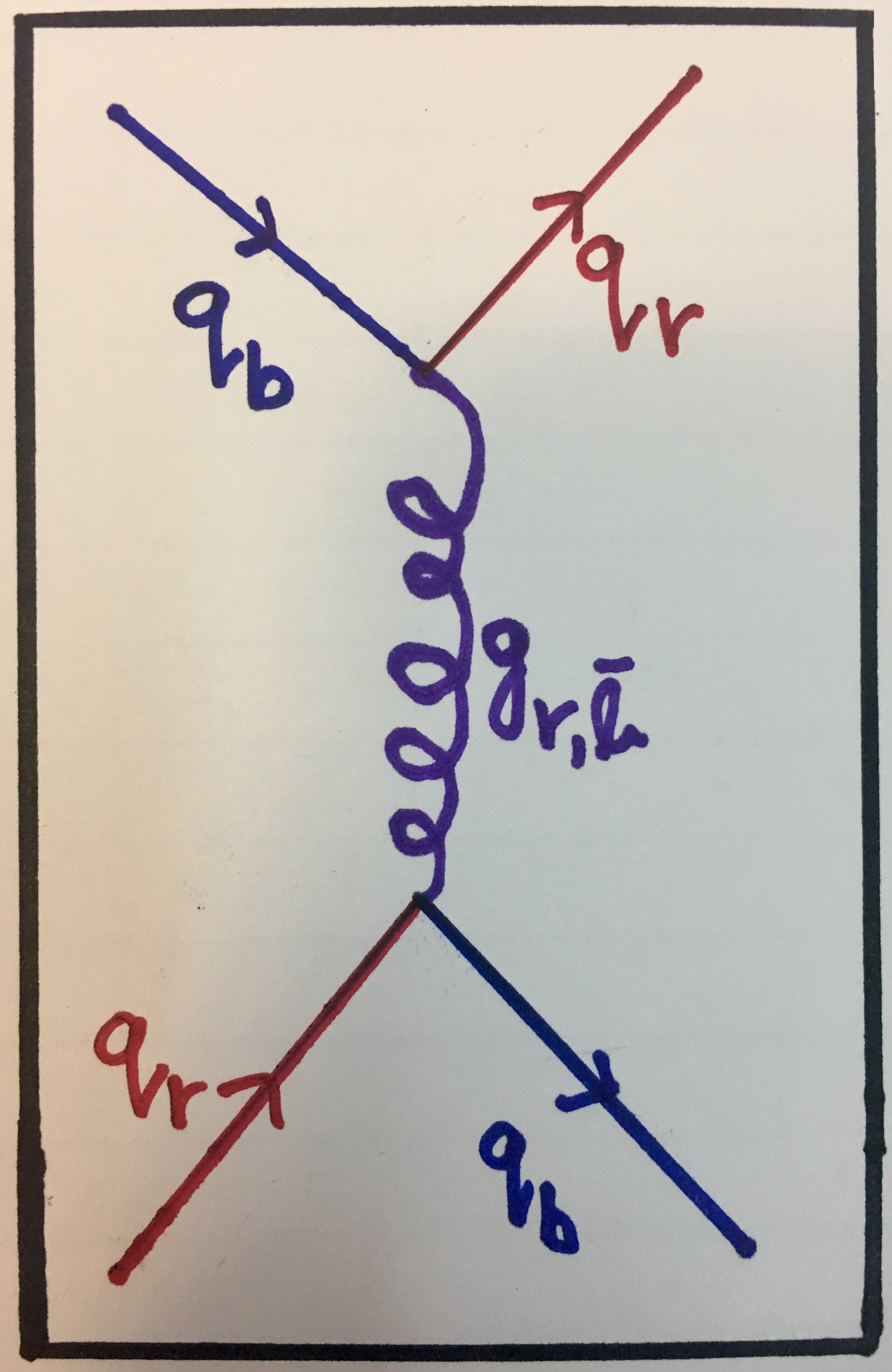
Feynman diagram showing gluon exchange between a red quark and a blue quark which swap colours when the interaction is over. This process is described in detail in the second part of the series: Colourful Quantum Chromodynamics.

There is one more Feynman diagram that you can draw. This is the one involving red and green quarks. I leave drawing this Feynman diagram as an exercise for you and I highly recommend you attempt it. It should be very analogous to the two diagrams you've already seen for this process.

Residual Strong Interaction

The second type of the strong interaction is the residual strong interaction, responsible for holding nucleons (like protons and neutrons) together inside the nucleus. Such an interaction is demonstrated in this animation:

Pion exchange in a nucleus binding a proton to a neutron. You can also notice gluon exchange between the quarks inside the nuclei as a result of the fundamental strong force acting.

Image from Wikipedia

We'll touch on some important points about this. Firstly, you should know that a meson is a particle composed of a quark-antiquark pair that need not be of the same quark flavour but must be colour opposites. The pions appearing and disappearing above are such a particle. In this case, the pions are neutral (π⁰) and consist of down-antidown quark pairs and they are indeed the mediators of this interaction. Something else also happens. Notice how just before the pion is emitted from one of the nucleons, a gluon essentially becomes a quark-antiquark pair. The antiquark joins with one of the quarks and forms the pion while the quark takes the place of the quark that is now part of the pion. If you think about it, this does not violate any conservation laws because the gluon carries two colour charges which become the charges of the two quarks. In addition quark flavour is conserved as the quark-antiquark pair are of the same flavour. You should also be able to tell that baryon number is conserved.

Why this happens relates to the energy associated with the colour fields of the strong interactions and is beyond the scope of this article. You may find this phenomenon somewhat analogous to pair production in the electromagnetic interaction but beware, as it is not exactly the case! Recall a major difference between the electromagnetic interaction and the strong interaction is that the mediators of the strong interaction (gluons and mesons) carry the charge of the interaction whereas those of the electromagnetic interaction (photons) do not.

Pair production and pair annihilation by the strong force

You may find the gluon splitting into a quark-antiquark pair described above analogous to when a photon spontaneously pair produces an electron-positron pair and indeed it somewhat is (but not exactly as described above)! And indeed, the opposite interaction (pair annihilation) can also happen. This can happen for any quark-antiquark pair that have the same flavour because quark flavour must be conserved. We can represent these interactions like this:

$g\stackrel{}{\to } q + \overline{q}$

$q + \overline{q}\stackrel{}{\to } g$

Top: a gluon pair producing a quark-antiquark pair. Bottom: a quark-antiquark pair annihilating into a gluon.

As you would expect, we can represent these also by Feynman diagrams:

Feynman diagram showing strong pair production. Notice how the colour charges (which are arbitrary here) are conserved.

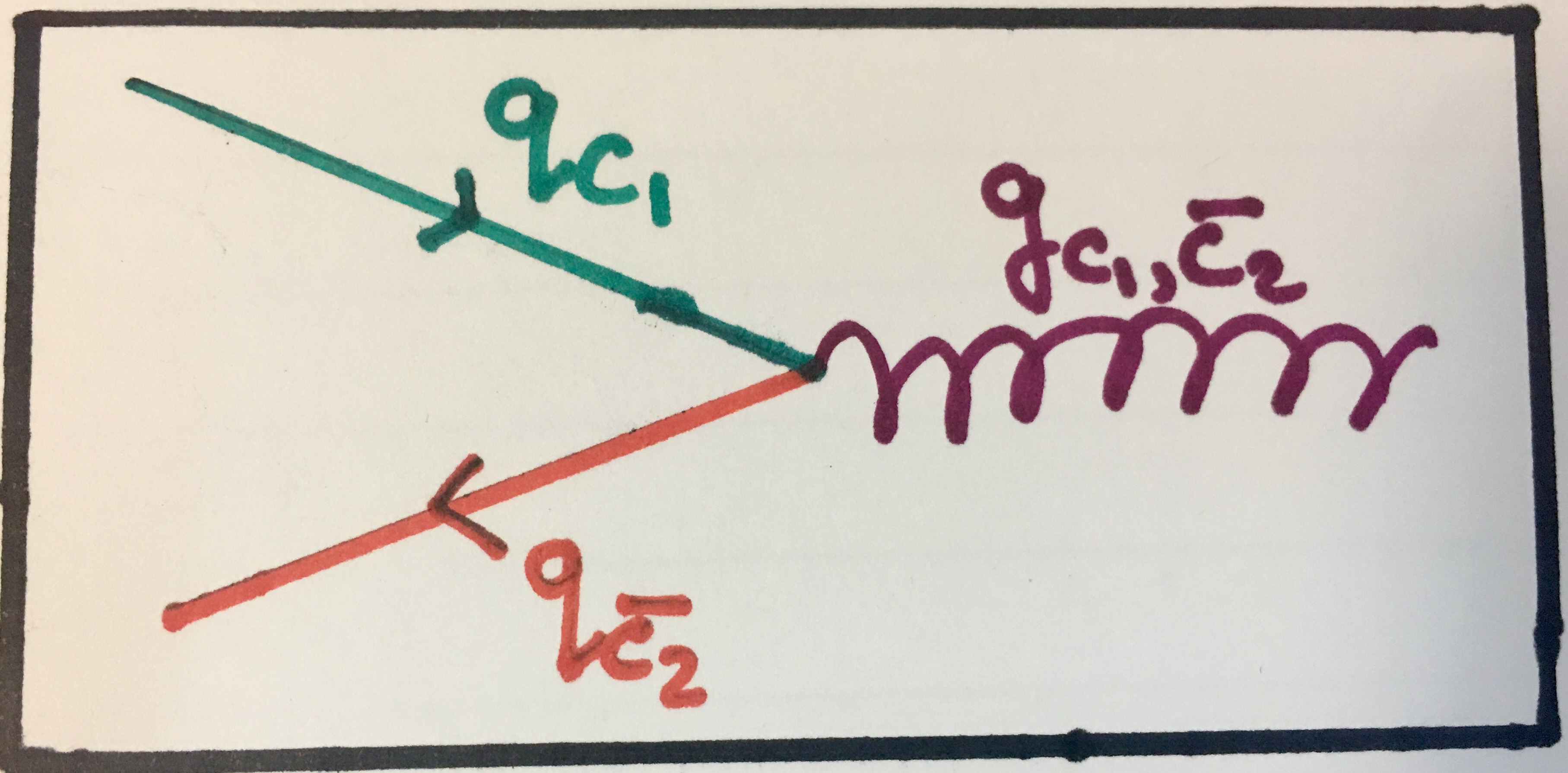
Feynman diagram showing strong pair annihilation. Again see how the colour charges are conserved across the vertex.

I kept this section regarding the strong interaction brief as I have talked about the details of the phenomena discussed above in the last part of this series. If you're interested in finding out more, you can find it here. Now we can move on to considering the weak nuclear interaction.

The Weak Nuclear Interaction

The weak nuclear interaction is the one responsible for important phenomena such as radioactive decay and nuclear fusion in the sun. It essentially explains the phenomena that the forces we considered so far can't. If you have read my article on symmetry, you will know that the weak interaction is the only one that does not conserve quark flavour. This is very important for phenomena which involve the transmutation of protons to neutrons and vice versa.

Note: The weak force quantum number

Analogous to the electric charge of the electromagnetic interaction and the colour charge of the strong interaction, the weak interaction also has an associated quantum number that is conserved in weak interactions. This is the weak isospin of particles. Because this is related to other concepts like the chirality and helicity of particles, I will not be tackling the conservation of this quantum number in the examples that we consider. Suffice it to say, all the fundamental particles which interact through the weak interaction do have this associated property and we will assume it is conserved in all the examples presented.

Neutrinos!

You may have noticed that, so far, we have not seen the neutrino appear in any of the interactions that we have considered. Indeed, neutrinos only interact weakly and gravitationally (very lightly, as their mass is very small). And this is where they make their debut in this article! They do not interact strongly as they do not carry colour charge nor do they interact electromagnetically because they do not carry electric charge. They do have weak isospin, however, so they do interact weakly. For the purposes of this article, they mostly come into play when it is needed to balance a lepton quantum number when electric charge is already balanced. This will become more clear when we consider examples.

Mediators of the weak interaction

The weak nuclear interaction is mediated by three bosons. These are the W⁺, W^- and Z⁰. The W⁺ and W^- bosons are the ones responsible for β+ and β- decay, respectively, as we'll see below. These actually carry electric charge (+1 and -1, respectively) so they do interact electromagnetically. The Z⁰ boson does not carry electric charge and usually decays into a particle-antiparticle pair. Now, let's see these bosons in action!

Examples

Example 1: Beta Decay

This is perhaps the most common and most important weak interaction. This is the process by which a neutron transmutates into a proton, releasing an electron and an electron antineutrino. The released electron is what we call a beta particle. This is β- decay. This interaction can also happen when a proton transmutates into a neutron releasing a positron and an electron neutrino and this is β+ decay.

By now, you should know that protons and neutrons are not fundamental particles as they are made up of quarks. Indeed this beta decay is better understood when we consider what's happening on the quark level. Let's think about the proton and neutron composition for a second. A proton is made up of two up quarks and a down quark. A neutron is made up of one up quark and two down quarks. So in order for a neutron to become a proton, one of the down quarks needs to become an up quark. Similarly, for a proton to become a neutron, one of the up quarks needs to become a down quark. Both of these operations (up to down and down to up) violate quark flavour conservation but that's fine as they occur through the weak interaction and emit W^- or W⁺ bosons.

We can write these interactions in the familiar notation like this:

$d\stackrel{}{\to } u + e^{-}+ \overline{{\nu }_e}$

$u\stackrel{}{\to } d + e^{+}+ \stackrel{}{{\nu }_e}$

Top: β- decay. The down quark becomes an up quark while emitting an electron and an electron antineutrino. Bottom: β+ decay. The up quark becomes a down quark while emitting a positron and an electron neutrino.

We can also now draw the Feynman diagrams for these interactions:

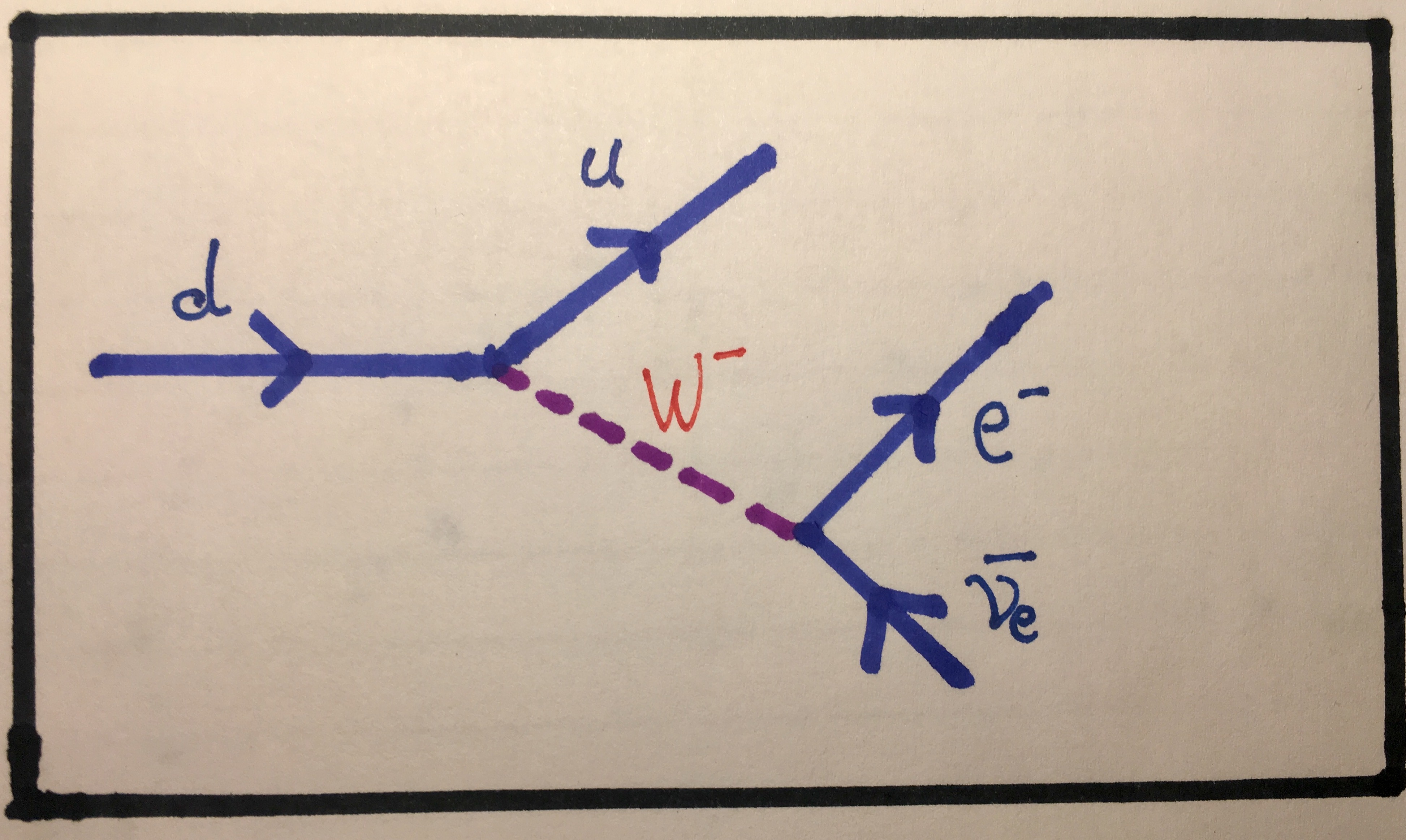
Feynman diagram showing a down quark transmutating into an up quark while emitting a W^- boson which then decays into an electron and an electron antineutrino. This is β- decay.

Feynman diagram showing an up quark transmutating into a down quark while emitting a W⁺ boson which then decays into a positron and an electron neutrino. This is β+ decay.

You should be able to see that across the two vertices involved in each diagram, electric charge is conserved. In the second vertex, the neutrino is necessary because the W bosons do not have an electron lepton number whereas the electron and the positron do. So the neutrino balances the electron lepton number of the electron or the positron.

Example 2: Decay of W bosons

In the previous example, we can indeed consider the second vertex alone, which shows the W bosons decaying into an electron or a positron and an antineutrino or a neutrino. This can indeed be generalised such that the W boson decays into any lepton-antineutrino or antilepton-neutrino pairs. A lepton-antineutrino pair would be emitted when a W^- boson decays and an antilepton-neutrino pair would be emitted when a W⁺ boson decays.

Here, I will show you the Feynman diagrams for a W^- decaying into a muon and a muon antineutrino and for a W⁺ decaying into an antitau and a tau neutrino. There are four other Feynman diagrams that we can draw for these interactions and I invite you to attempt drawing them. We can write these two decays like this:

$W^{-}\stackrel{}{\to } {\mu }^{-}+ \overline{{\nu }_{\mu }}$

$W^{+}\stackrel{}{\to } {\tau }^{+}+ \stackrel{}{{\nu }_{\tau }}$

Top: W^- decays into a muon and a muon antineutrino. Bottom: W⁺ decays into an antitau and a tau neutrino.

And here are the Feynman diagrams corresponding to these interactions:

A W^- boson decays into a muon and a muon antineutrino.

A W⁺ boson decays into an antitau lepton and a tau neutrino.

Example 3: Z⁰ decay

The Z⁰ boson can theoretically decay into any particle-antiparticle pair. This includes neutrinos as they carry weak isospin and, as such, interact weakly, as discussed above. We will consider Z⁰ bosons decaying into lepton-antilepton pairs, neutrino-antineutrino pairs and quark-antiquark pairs. We can write these interactions down (where l represents any lepton, q represents any quark and ν represents any neutrino) like this:

$Z^0\stackrel{}{\to } l+\stackrel{\_}{l}$

$Z^0\stackrel{}{\to } {\nu }_{}+\stackrel{\_}{{\nu }_{}}$

$Z^0\stackrel{}{\to } q+\stackrel{\_}{q}$

Top: a Z⁰ decays into any lepton-antilepton pair. Middle: a Z⁰ decays into any neutrino-antineutrino pair. Bottom: a Z⁰ decays into any quark-antiquark pair.

Below, you can see the Feynman diagram for the first of these interactions. I again invite you to draw the Feynman diagrams for the two other interactions, which should be very similar to the one shown here:

A Z⁰ boson decays into any lepton and antilepton.

Example 4: Proton-proton fusion

This is the procedure by which two protons fuse and undergo a process that ends in the release of an alpha particle and two other protons, thus starting the process again. An alpha particle is simply a helium nucleus; two protons and two neutrons. I will not consider the entire process here, but I would just like to point out that one of the steps involves a proton transmutating to become a neutron, releasing a positron and an electron neutrino through the weak interaction. We have considered this above in the beta decay section and have identified it as β+ decay, but I would like to show you the Feynman diagram for the process involving the proton and the neutron. For starters, we can represent this interaction in the usual notation like this:

$p\stackrel{}{\to } n + e^{+}+ {\nu }_e$

A proton transmutating into a neutron, releasing a positron and an electron neutrino.

And here is the Feynman diagram corresponding to this interaction:

A proton transmutating into a neutron through weak decay. Notice the notation in how the compositions of the non-fundamental particles (the proton and the neutron) are represented in the Feynman diagram.

Conclusion

The has been a rather lengthy article as we've considered many examples in detail. However, this is still just a brief introduction to one of the most important aspects of particle physics. I hope you have found this read informative as well as entertaining!

Something to do about Feynman diagrams

As a general exercise about what we've covered here, I invite you to start drawing up your own Feynman diagrams for interactions that you think about. To start, ask yourself this: what particles do I want to have initially and what particles do I want the interaction to end with? Is there any possible path through which this could happen? Is there more than one? Keep in mind the importance of making sure that conservation laws are obeyed.

If you do do this, feel free to let me know how it went. You can leave a comment below, tweet me or send me a message through the website.

What's next?

I think I might take a short break from writing about physics now to focus on other things (like building The Standard Model app). I still have ideas for things to write, and I will return eventually.

Closing Remarks

Thank you very much for reading! If you enjoyed reading this part of Particle Physics or if there's something you'd like done better next time, please feel free to contact me through the website, send me a tweet or leave a comment on this page. Your feedback would be very much appreciated and will help improve the coming articles.

Thanks!